题目内容
20.下列方程是一元二次方程的是( )| A. | (x-1)(x+2)=x2+3 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}-2$=0 | C. | (x-1)2=2x-2 | D. | ax2+2x-1=0 |
分析 根据一元二次方程的定义解答.一元二次方程必须满足四个条件:(1)未知数的最高次数是2;(2)二次项系数不为0;(3)是整式方程;(4)含有一个未知数.由这四个条件对四个选项进行验证.
解答 解:A、是一元一次方程,故A错误;
B、是分式方程,故B错误;
C、是一元二次方程,故C正确;
D、a=0时是一元一次方程,故D错误;
故选:C.
点评 本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
11.某城市2012年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2014年底增加到363公顷,设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )
| A. | 300(1+x)=363 | B. | 300(1+x)2=363 | C. | 300(1+2x)=363 | D. | 363(1-x)2=300 |
8.下列各组条件中,不能判断△ABC≌△DEF的是( )
| A. | ∠A=∠D,AB=DE,∠B=∠E | B. | AB=DE,∠A=∠D,BC=EF | ||
| C. | AB=DE,BC=EF,AC=DF | D. | ∠B=∠E=90°,AB=DE,AC=DF |
15.二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0解为( )
| A. | x1=-3 x2=-1 | B. | x1=1 x2=3 | C. | x1=-1 x2=3 | D. | x1=-3 x2=1 |
9.三角形两边的长是3和4,第三边的长是方程x2-10x+21=0的根,则该三角形的周长为( )
| A. | 14 | B. | 10 | C. | 10或14 | D. | 以上都不对 |
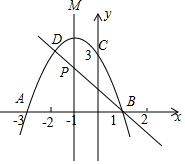 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D. 为了促进节能减排,促进节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了三个档次每户每月电费y(元)与用电量x(度)间的函数关系,在每月用电量超过230度时,每多用1度电要比第一档多付电费m元,且此时每户每月电费y(元)与用电量x(度)间的函数关系y=kx-64.5,则m=0.17.
为了促进节能减排,促进节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了三个档次每户每月电费y(元)与用电量x(度)间的函数关系,在每月用电量超过230度时,每多用1度电要比第一档多付电费m元,且此时每户每月电费y(元)与用电量x(度)间的函数关系y=kx-64.5,则m=0.17.