题目内容
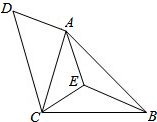 如图所示,在△ABC中,BE是∠ABC的平分线,且∠BCE=∠EAB,过C作CD∥AE,连接AC,求证:CA是∠DCE的平分线.
如图所示,在△ABC中,BE是∠ABC的平分线,且∠BCE=∠EAB,过C作CD∥AE,连接AC,求证:CA是∠DCE的平分线.考点:全等三角形的判定与性质,平行线的性质
专题:证明题
分析:求出∠ABE=∠CBE,根据AAS推出△ABE≌△CBE,推出AE=EC,推出∠EAC=∠ECA,∠DCA=∠EAC,即可得出答案.
解答:证明:∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
在△ABE和△CBE中
∴△ABE≌△CBE(AAS),
∴AE=EC,
∴∠EAC=∠ECA,
∵CD∥AE,
∴∠DCA=∠EAC,
∴∠DCA=∠ECA,
即CA是∠DCE的平分线.
∴∠ABE=∠CBE,
在△ABE和△CBE中
|
∴△ABE≌△CBE(AAS),
∴AE=EC,
∴∠EAC=∠ECA,
∵CD∥AE,
∴∠DCA=∠EAC,
∴∠DCA=∠ECA,
即CA是∠DCE的平分线.
点评:本题考查了等腰三角形的性质,全等三角形的性质和判定,平行线的性质的应用,解此题的关键是推出∠EAC=∠ECA和∠DCA=∠EAC,题目比较好,难度适中.

练习册系列答案
相关题目
下列各单项式中,与2x4y是同类项的为( )
| A、2x4 |
| B、2xy |
| C、x4y |
| D、2x2y3 |
 如图,在矩形ABCD中,沿直线AE把三角形ADE折叠,使点D恰好落在边BC上一点F处,AB=8cm,CE=3cm,求BF的长度.
如图,在矩形ABCD中,沿直线AE把三角形ADE折叠,使点D恰好落在边BC上一点F处,AB=8cm,CE=3cm,求BF的长度.