题目内容
已知抛物线y=x2-4x+h的顶点A在直线y=-4x-1上,求抛物线的顶点坐标.
考点:二次函数的性质
专题:
分析:根据抛物线解析式求出顶点坐标,然后代入直线解析式计算求出h的值,再求解即可.
解答:解:∵抛物线y=x2-4x+h的顶点坐标为x=-
=2,y=
=h-4,
∴A(2,h-4).
∵点A在直线y=-4x-1上,
∴h-4=-8-1=-9,
∴A(2,-9).
| -4 |
| 2 |
| 4×1×h-(-4)2 |
| 4×1 |
∴A(2,h-4).
∵点A在直线y=-4x-1上,
∴h-4=-8-1=-9,
∴A(2,-9).
点评:本题考查了二次函数的性质,一次函数图象上点的坐标特征,用h表示出抛物线的顶点坐标是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 如图,△ABC中,D是BC延长线上一点,CE平分∠ACB且CE∥AD,F是AD的中点,连结CF,求证:CF⊥AD.
如图,△ABC中,D是BC延长线上一点,CE平分∠ACB且CE∥AD,F是AD的中点,连结CF,求证:CF⊥AD.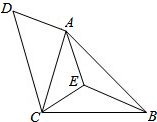 如图所示,在△ABC中,BE是∠ABC的平分线,且∠BCE=∠EAB,过C作CD∥AE,连接AC,求证:CA是∠DCE的平分线.
如图所示,在△ABC中,BE是∠ABC的平分线,且∠BCE=∠EAB,过C作CD∥AE,连接AC,求证:CA是∠DCE的平分线. 如图,根据下面的条件和图中所标出的角,分别写出所有正确的结论,并从中选出一个加以证明.
如图,根据下面的条件和图中所标出的角,分别写出所有正确的结论,并从中选出一个加以证明.