题目内容
6.已知A市出租车原收费标准如下:不超过3km的路程按起步价10元收费,超过3km以外的路程按2.4元/km收费.为了减少出租车空车返回的损失,现A市决定实施返空费方案,设出租车行驶的路程为xkm,具体方案如下:当0<x≤20时,按原收费标准收费;当x>20时,在原收费标准基础上,再加收0.01x元/km.例如,当出租车行驶了50km时,收费总额为:2.4×(50-3)+10+(0.01×50)×(50-20)=137.8(元).(1)A市实施返空费方案后,当x>20时,求收费总额y(元)与x(km)的函数关系式;
(2)自4月1日起,南京市实施的返空费方案是:不超过20km的路程,与A市的原收费标准相同;超过20km以外的路程,按原单价2.4元/km的1.5倍收费.若行驶路程x超过20km,分别按两市返空费方案计算,当收费总额相同时,求x的值.
分析 (1)根据题意可得:A市实施返空费方案后,当x>20时,收费总额y(元)与x(km)的函数关系式为y=2.4×(x-3)+10+0.01x(x-20);
(2)当x>20时,表示出南京市收费总额y(元)与x(km)的函数关系式为:y=10+2.4×(20-3)+2.4×1.5×(x-20)=3.6x-21.2,根据收费总额相同,列出方程0.01x2+2.2x+2.8=3.6x-21.2,即可解答.
解答 解:(1)A市实施返空费方案后,当x>20时,收费总额y(元)与x(km)的函数关系式为:
y=2.4×(x-3)+10+0.01x(x-20)=0.01x2+2.2x+2.8;
(2)当x>20时,南京市收费总额y(元)与x(km)的函数关系式为:
y=10+2.4×(20-3)+2.4×1.5×(x-20)=3.6x-21.2,
当收费总额相同时,即0.01x2+2.2x+2.8=3.6x-21.2,
整理得:x2-140x+2400=0,
即(x-120)(x-20)=0,
解得:x1=120,x2=20,
∵x>20,
∴x=120,
即当收费总额相同时,x=120.
点评 本题考查了一次函数的应用,解决本题的关键是得到当x>20时,收费总额y(元)与x(km)的函数关系式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.(1)$\sqrt{18}$×$\sqrt{\frac{1}{2}}$÷$\sqrt{3}$
(2)$\sqrt{8}$+2$\sqrt{3}$-($\sqrt{27}$-$\sqrt{2}$)
(2)$\sqrt{8}$+2$\sqrt{3}$-($\sqrt{27}$-$\sqrt{2}$)
1.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
| A. | 方差是8.02 | B. | 中位数是9 | C. | 众数是5 | D. | 极差是9 |
18.下列说法中,不正确的是( )
| A. | 同位角相等,两直线平行 | |
| B. | 两直线被第三条直线所截,内错角相等 | |
| C. | 两直线平行,内错角相等 | |
| D. | 同旁内角互补,两直线平行 |
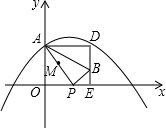 如图,在平面直角坐标系xOy中,抛物线y=ax2+$\frac{5}{6}$x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+$\frac{5}{6}$x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.