题目内容
15．a为方程x2-x-3=0的一个根，求$\frac{1}{a}$-$\frac{1}{a-1}$=-$\frac{1}{3}$．分析 根据一元二次方程的解的定义得a2=a+3，再把$\frac{1}{a}$-$\frac{1}{a-1}$通分后计算得到-$\frac{1}{{a}^{2}-a}$，然后利用整体代入的方法计算．
解答 解：∵a为方程x2-x-3=0的一个根，
∴a2-a-3=0，
∴a2=a+3，
∴$\frac{1}{a}$-$\frac{1}{a-1}$=$\frac{a-1-a}{a（a-1）}$=-$\frac{1}{{a}^{2}-a}$=-$\frac{1}{3}$．
故答案为-$\frac{1}{3}$．
点评 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
1．
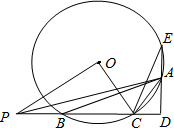如图，△ABC内接于⊙O，AD⊥BC于D交⊙O于E
（1）若∠ACB=120°，求证：CE=⊙O的半径．
（2）连OC，OP⊥OC交CB的延长线于P，若⊙O的半径为5cm，弦BC=6cm，求PB的长．
如图，△ABC内接于⊙O，AD⊥BC于D交⊙O于E（1）若∠ACB=120°，求证：CE=⊙O的半径．
（2）连OC，OP⊥OC交CB的延长线于P，若⊙O的半径为5cm，弦BC=6cm，求PB的长．
2．
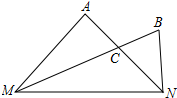如图，在MN的同侧作△AMN和△BMN，BM平分∠AMN，AN平分∠BNM，AN交BM于点C．设∠A=α°，∠B=β°，下列结论不正确的是（ ）
如图，在MN的同侧作△AMN和△BMN，BM平分∠AMN，AN平分∠BNM，AN交BM于点C．设∠A=α°，∠B=β°，下列结论不正确的是（ ）| A． | 若α=β，则点C在MN的垂直平分线上 | |
| B． | 若α+β=180°，则∠AMB=∠NMB | |
| C． | ∠MCN=$（\frac{α+β}{3}+60）$° | |
| D． | 当∠MCN=120°时，延长MA、NB交于点O，则OA=OB |