题目内容
14.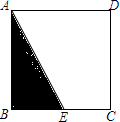 某人定制了一批如图所示的地砖,每块地砖都是边长为(x+3y)米的正方形,点E在正方形ABCD的边BC上,EC=(x+y)米,已知x+3y=5米,x+2y=4米,求四边形AECD的面积.
某人定制了一批如图所示的地砖,每块地砖都是边长为(x+3y)米的正方形,点E在正方形ABCD的边BC上,EC=(x+y)米,已知x+3y=5米,x+2y=4米,求四边形AECD的面积.
分析 首先由x+3y=5米,x+2y=4米,建立方程组求得x、y,进一步得出AD、CD、CE的长,利用梯形的面积计算方法得出答案即可.
解答 解:由题意得
$\left\{\begin{array}{l}{x+3y=5}\\{x+2y=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
则AD=CD=x+3y=5,CE=x+y=3,
四边形AECD的面积=$\frac{1}{2}$×(3+5)×5=20平方米.
点评 此题考查二元一次方程组的实际运用,掌握二元一次方程组的解法和四边形的面积计算方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知四边形ABCD中,AC、BD相交于O,AB∥CD,则添加下列哪一个条件后,仍无法判定△AOB与△COD全等( )
| A. | AB=CD | B. | AD=BC | C. | AD∥BC | D. | OA=OC |
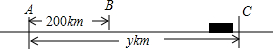 用函数表达式表示下列变化过程中两个变量之间的关系,并指出其中的一次函数、正比例函数.
用函数表达式表示下列变化过程中两个变量之间的关系,并指出其中的一次函数、正比例函数.