题目内容
5．
已知△ABC的面积为1，把它的各边延长一倍得△A1B1C1；再△A1B1C1的各边延长两倍得△A2B2C2；在△A2B2C2的各边延长三倍得△A3B3C3，△A3B3C3的面积为4921．
分析 先根据根据等底的三角形高的比等于面积比求出△A1B1C1及△A2B2C2的面积，再根据两三角形的倍数关系求解即可．
解答 解：△ABC与△A1BB1底相等（AB=A1B），高为1：2（BB1=2BC），故面积比为1：2，
∵△ABC面积为1，
∴S△A1B1B=2．
同理可得，S△C1B1C=2，S△AA1C=2，
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7；
如图，连接A2C1，
根据A2B1=2A1B1，得到：A1B1：A2A1=1：3，
因而若过点B1，A2作△A1B1C1与△A1A2C1的A1C1边上的高，则高线的比是1：3，
因而面积的比是1：3，则△A2B1C1的面积是△A1B1C1的面积的2倍，
则△A2B1C1的面积是14，
同理可以得到△A2B2C1的面积是△A2B1C1面积的2倍，是28，
则△A2B2B1的面积是42，
同理△B2C2C1和△A2C2A1的面积都是42，
△A2B2C2的面积是7×19=133，
同理△A3B3C3的面积是7×19×37=4921，
故答案为：4921．
点评 考查了三角形的面积，正确判断相邻的两个三角形面积之间的关系是解决本题的关键．
练习册系列答案
相关题目
15．抛物线y=-2（x-1）2+3的顶点坐标是（ ）
| A． | （-1，3） | B． | （1，3） | C． | （1，-3） | D． | （-1，-3） |
如图，已知一次函数y=2x+2的图象与y轴交于点B，与反比例函数y=$\frac{{k}_{1}}{x}$的图象的一个交点为A（1，m），过点B作AB的垂线BD，与反比例函数y=$\frac{{k}_{2}}{x}$（x＞0）的图象交于点D（n，-2）．
10．
如图，在平面直角坐标系中，从点P1（-1，0），P2（-1，-1），P3（1，-1），P4（1，1），P5（-2，1），P6（-2，-2），…依次扩展下去，则P2017的坐标为（ ）
如图，在平面直角坐标系中，从点P1（-1，0），P2（-1，-1），P3（1，-1），P4（1，1），P5（-2，1），P6（-2，-2），…依次扩展下去，则P2017的坐标为（ ）| A． | （504，-504） | B． | （-504，504） | C． | （-504，503） | D． | （-505，504） |
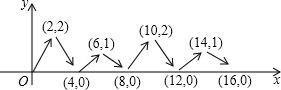如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（2，2），第2次接着运动到点（4，0），第3次接着运动到点（6，1），…，按这样的运动规律，经过第36次运动后，动点P的坐标是（72，0）．
如图，在平行四边形ABCD中，E、F为对角线AC上两点，且AE=CF，请你从图中找出一对全等三角形，并给予证明．