题目内容
9.a表示一个两位数,b表示一个三位数,若把a放在b的左边组成一个五位数记为m1,把b放在a的左边组成一个五位数记为m2,求证:m1-m2是9的倍数.分析 首先表示出m1和m2,然后把m1-m2分解成9为因数的式子即可证明.
解答 解:m1=1000a+b,m2=100b+a,
则m1-m2=(1000a+b)-(100b+a)
=999a-99b
=9(111a-11b).
则m1-m2是9的倍数.
点评 本题考查了整式的加减运算,正确表示出m1和m2是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列说法中不正确的是( )
| A. | 不是负数的数就是正数或0 | |
| B. | 负数有无限多个 | |
| C. | 正数和负数可以用来表示相反意义的量 | |
| D. | 零下3℃记作零下-3℃ |
18.观察下列前三个式子:$\sqrt{{3}^{2}-1}$=$\sqrt{2}$×$\sqrt{4}$,$\sqrt{{4}^{2}-1}$=$\sqrt{3}$×$\sqrt{5}$,$\sqrt{{5}^{2}-1}$=$\sqrt{4}$×$\sqrt{6}$,…,按照这样的规律第10个式子的结果是( )
| A. | $\sqrt{9}$×$\sqrt{11}$ | B. | $\sqrt{10}$×$\sqrt{12}$ | C. | $\sqrt{11}$×$\sqrt{13}$ | D. | $\sqrt{12}$×$\sqrt{14}$ |
19.已知菱形的周长是16,一边上的高是6,则菱形的面积是( )
| A. | 12 | B. | 24 | C. | 48 | D. | 64 |
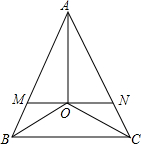 (1)如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB、AC于M、N,图中有几个等腰三角形?
(1)如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB、AC于M、N,图中有几个等腰三角形?