��Ŀ����
7������������֪ͼ��G1��G2����G1����ȡһ��P����G2����ȡһ��Q�����߶�PQ�ij�����Сʱ�����dz������С�ij���Ϊͼ��G1��G2�ġ��ܾࡱ�����߶�PQ�ij������ֵʱ�����dz�������ij���Ϊͼ��G1��G2�ġ���ࡱ��
������ѧϰ��������������Ļ����ϣ������������⣻
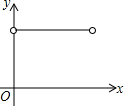
��ƽ��ֱ������ϵxOy�У���A������Ϊ��-3��4������B������Ϊ��3��4��������ABCD�ĶԳ�����Ϊ��O��
��1���߶�AD��BC�ġ��ܾࡱ��6������ࡱ��10��
��2����ֱ��y=-$\frac{3}{4}$x+b��b��0����x�ᡢy��ֱ��ڵ�E��F�����߶�EF�����ABCD�ġ��ܾࡱ��1�������ǵġ���ࡱ��
��3��ƽ��ֱ������ϵxOy����һ���ı���KLMN��������ABCD�Ƶ�O��תһ�ܣ�����ת�����У������ı���KLMN�ġ���ࡱ�����ֵΪ4$\sqrt{2}$+2����ת�����У������ı���KLMN�ġ��ܾࡱ��ȡֵ��Χ��6-4$\sqrt{2}$���ܾ��8-4$\sqrt{2}$��
���� ��1���߶�AD��BC�ġ��ܾࡱ��AB��DC�ij��ȣ�
��2�������ֱ��OA�Ľ���ʽ����ֱ֪��EF��OA��ֱ���ʵ�C��ֱ��EF�ľ���Ϊ����ࡱ��
��3������ͼ��O��K��D��һ��ֱ����ʱ���ܾ�����Сֵ����OK��ADʱ���ܾ������ֵ��
�ڵ��ı���KLMNΪ������ʱ��������ֵ��
��� �⣺��1����ͼ1��
�ɴ��ߵ����ʿ�֪���߶�AD��BC�ġ��ܾࡱ��AB��DC�ij��ȣ��ʡ��ܾࡱ��6��
��Rt��ADC�У�AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10������ࡱ��10��
�ʴ�Ϊ��6��10��
��2������ͼ��
��ֱ��OB�Ľ���ʽΪy=kx��
��x=3��y=4���뺯���Ľ���ʽ��4=3k�����k=$\frac{4}{3}$��
��ֱ��EF�Ľ���ʽΪy=-$\frac{3}{4}$x+b��
��ֱ��OB��EF���ֱ��
��EF�����ABCD�ġ��ܾࡱ��1��
���D��EF�ľ����=10+1=11��������ࡱ=11��
��3���ٵ�K��BD��ʱ����ͼ3��
����ABCD���ı���KLMN�ġ���ࡱΪKB=4$\sqrt{2}$+2��
��KD=BD-BK=10-��4$\sqrt{2}$+2��=8-4$\sqrt{2}$��������ܾ�=8-4$\sqrt{2}$��
�ڵ�OK��ADʱ����ͼ4��
����ABCD���ı���KLMN�ġ��ܾࡱ����Сֵ��
�߾��εĿ�Ϊ6��
��O��AD�ľ���Ϊ3��
���ɢٿ�֪OK=OD-KD=5-��8-4$\sqrt{2}$��=4$\sqrt{2}$-3��
�����ܾ����Сֵ=3-OK=3-��4$\sqrt{2}$-3��=6-4$\sqrt{2}$��
���ܾ�ķ�ΧΪ��6-4$\sqrt{2}$���ܾ��8-4$\sqrt{2}$��
�ʴ�Ϊ��6-4$\sqrt{2}$���ܾ��8-4$\sqrt{2}$��
���� ������Ҫ�������һ�κ����������ľ���͵㵽ֱ�ߵľ����Ӧ�ã����ⶨ�壬�������⻭��ͼ���ǽ���Ĺؼ�����Ŀ��Ϊ��ӱ���Ѷ����У�

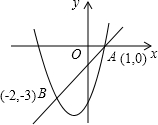 ��ͼ�����κ���y1=ax2+bx+c��һ�κ���y2=kx+b��ͼ����A��1��0����B��-2��-3�����㣬��y1��y2����x��ȡֵ��Χ�ǣ�������
��ͼ�����κ���y1=ax2+bx+c��һ�κ���y2=kx+b��ͼ����A��1��0����B��-2��-3�����㣬��y1��y2����x��ȡֵ��Χ�ǣ�������| A�� | x��-2 | B�� | -2��x��1 | C�� | x��1 | D�� | x��-2��x��1 |
 ����ô
����ô =_______��
=_______��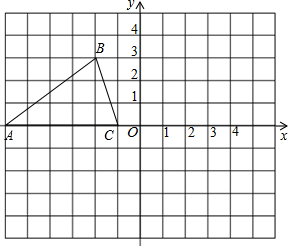 ��ͼ����֪��ABC���������������ֱ�ΪA��-6��0����B��-2��3����C��-1��0����
��ͼ����֪��ABC���������������ֱ�ΪA��-6��0����B��-2��3����C��-1��0����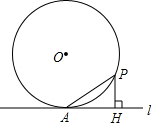 ��ͼ�����뾶Ϊ6��ԲO��һ��A��ԲO������l��PΪԲO��һ�����㣬��PH��l�ڵ�H������PA�����PA=x��AH=y����ô����ͼ���У��ܴ��±�ʾy��x�ĺ�����ϵ���ǣ�������
��ͼ�����뾶Ϊ6��ԲO��һ��A��ԲO������l��PΪԲO��һ�����㣬��PH��l�ڵ�H������PA�����PA=x��AH=y����ô����ͼ���У��ܴ��±�ʾy��x�ĺ�����ϵ���ǣ�������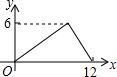
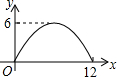
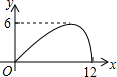
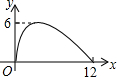
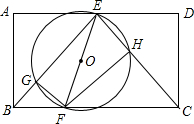 ��ͼ������ABCD�У�EΪAD�е㣬��FΪBC�ϵĶ��㣨����B��C�غϣ�������EF����EFΪֱ����Բ�ֱ�BE��CE�ڵ�G��H����BF�ij���Ϊx����FG��FH�ij��Ⱥ�Ϊy��������ͼ���У��ܱ�ʾy��x֮��ĺ�����ϵ��ͼ������ǣ�������
��ͼ������ABCD�У�EΪAD�е㣬��FΪBC�ϵĶ��㣨����B��C�غϣ�������EF����EFΪֱ����Բ�ֱ�BE��CE�ڵ�G��H����BF�ij���Ϊx����FG��FH�ij��Ⱥ�Ϊy��������ͼ���У��ܱ�ʾy��x֮��ĺ�����ϵ��ͼ������ǣ�������
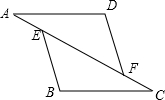 ��ͼ����A��E��F��C��ͬһֱ���ϣ�AD��BC��AD=CB��AE=CF����֤��BE��DF��
��ͼ����A��E��F��C��ͬһֱ���ϣ�AD��BC��AD=CB��AE=CF����֤��BE��DF��