题目内容
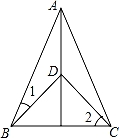
如图,点A和点D都在线段BC的垂直平分线上.连接AB,AC,DB,DC.如果∠1=20°,∠2=50°.那么∠BAC比∠BDC( )
A.大40° B.小40° C.大30° D.小30°
B【考点】线段垂直平分线的性质.
【分析】根据线段垂直平分线的性质得到AB=AC,DB=DC,由等腰三角形的性质得到∠ABC=∠ACB,∠DBC=∠2=50°,根据三角形的内角和得到∠BAC=40°,∠BDC=80°,即可得到结论.
【解答】解:∵点A和点D都在线段BC的垂直平分线上,
∴AB=AC,DB=DC,
∴∠ABC=∠ACB,∠DBC=∠2=50°,
∴∠ABC=∠ACB=∠1+∠DBC=70°,
∴∠BAC=40°,∠BDC=80°,
∴∠BAC比∠BDC小40°,
故选B.
【点评】本题考查了线段垂直平分线的性质,等腰三角形的性质,三角形的内角和,熟练掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
相关题目
在一次数学课上,李老师出示一道题目:
| 如图,在△ABC中,AC=BC,AD=BD,∠A=30°,在线段AB上求作两点P,Q,使AP=CP=CQ=BQ. |
明明作法:分别作∠ACD和∠BCD的平分线,交AB于点P,Q.点P,Q就是所求作的点.
晓晓作法:分别作AC和BC的垂直平分线,交AB于点P,Q.点P,Q就是所求作的点.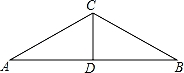
你认为明明和晓晓作法正确的是( )
A.明明 B.晓晓 C.两人都正确 D.两人都错误
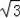
 cm,求弦AE的长.
cm,求弦AE的长.

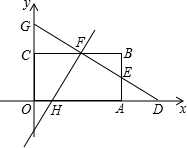
 ;
;
 x2+
x2+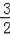

 B.
B.