题目内容
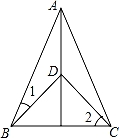
如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2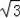
 cm,求弦AE的长.
cm,求弦AE的长.


【考点】切线的判定.
【分析】(1)连接OC,由等腰三角形的性质和角平分线得出∠2=∠3,证出∴OC∥AD,再由已知条件得出CD⊥OC,即可得出结论;
(2)作OF⊥AE于F,则AF=
 AE,四边形OFDC是矩形,得出OF=CD=2
AE,四边形OFDC是矩形,得出OF=CD=2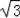
 cm,由勾股定理求出AF,即可得出AE的长.
cm,由勾股定理求出AF,即可得出AE的长.
【解答】(1)证明:连接OC,如图所示:
∵OA=OC,
∴∠1=∠3,
∵AC平分∠BAD,
∴∠1=∠2,
∴∠2=∠3,
∴OC∥AD,
∵CD⊥AD,
∴CD⊥OC,
∴CD为⊙O的切线;
(2)解:作OF⊥AE于F,如图2所示:
则AF=
 AE,四边形OFDC是矩形,
AE,四边形OFDC是矩形,
∴OF=CD=2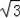
 cm,
cm,
∵OA=
 AB=4cm,
AB=4cm,
∴AF=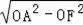
 =
=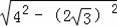
 =2,
=2,
∴AE=2AF=4.
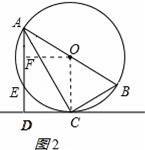

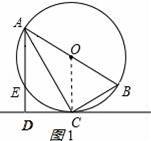

【点评】本题考查了切线的判定、等腰三角形的性质、平行线的判定与性质、矩形的判定与性质、垂径定理、勾股定理等知识;本题综合性强,熟练掌握切线的判定和垂径定理是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目