题目内容
.已知抛物线y=﹣
 x2+
x2+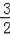
 x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为( )
x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为( )
A.
 B.
B.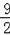
 C.
C.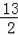
 D.
D.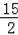

D【考点】抛物线与x轴的交点.
【专题】压轴题.
【分析】令y=0,则﹣
 x2+
x2+
 x+6=0,由此得到A、B两点坐标,由D为AB的中点,知OD的长,x=0时,y=6,所以OC=6,根据勾股定理求出CD即可.
x+6=0,由此得到A、B两点坐标,由D为AB的中点,知OD的长,x=0时,y=6,所以OC=6,根据勾股定理求出CD即可.
【解答】解:令y=0,则﹣
 x2+
x2+
 x+6=0,
x+6=0,
解得:x1=12,x2=﹣3
∴A、B两点坐标分别为(12,0)(﹣3,0)
∵D为AB的中点,
∴D(4.5,0),
∴OD=4.5,
当x=0时,y=6,
∴OC=6,
∴CD=
 =
=
 .
.
故选:D.
【点评】本题主要考查了二次函数与一元二次方程的关系和抛物线的对称性,求出AB中点D的坐标是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 2+ 3x +4=0
2+ 3x +4=0