Question

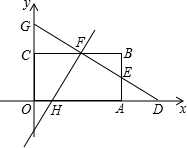
如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A、C分别在坐标轴上，顶点B的坐标为（6，4），E为AB的中点，过点D（8，0）和点E的直线分别与BC、y轴交于点F、G．

（1）求直线DE的函数关系式；

（2）函数y=mx﹣2的图象经过点F且与x轴交于点H，求出点F的坐标和m值；

（3）在（2）的条件下，求出四边形OHFG的面积．

Answer 1

【考点】一次函数综合题．

【分析】（1）由顶点B的坐标为（6，4），E为AB的中点，可求得点E的坐标，又由过点D（8，0），利用待定系数法即可求得直线DE的函数关系式；

（2）由（1）可求得点F的坐标，又由函数y=mx﹣2的图象经过点F，利用待定系数法即可求得m值；

（3）首先可求得点H与G的坐标，即可求得CG，OC，CF，OH的长，然后由S_{四边形OHFG}=S_梯形OHFC+S_△CFG，求得答案．

【解答】解：（1）设直线DE的解析式为：y=kx+b，

∵顶点B的坐标为（6，4），E为AB的中点，

∴点E的坐标为：（6，2），

∵D（8，0），

∴，

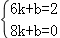解得：，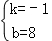

∴直线DE的函数关系式为：y=﹣x+8；

（2）∵点F的纵坐标为4，且点F在直线DE上，

∴﹣x+8=4，

解得：x=4，

∴点F的坐标为；（4，4）；

∵函数y=mx﹣2的图象经过点F，

∴4m﹣2=4，

解得：m=；

（3）由（2）得：直线FH的解析式为：y=x﹣2，

∵x﹣2=0，

解得：x=，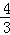

∴点H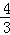（，0），

∵G是直线DE与y轴的交点，

∴点G（0，8），

∴OH=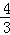，CF=4，OC=4，CG=OG﹣OC=4，

∴S_{四边形OHFG}=S_梯形OHFC+S_△CFG=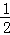×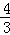（+4）×4+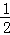×4×4=18．

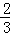【点评】此题考查了待定系数法求一次函数的解析式、中点坐标的求解方法以及多边形的面积问题．此题难度较大，注意掌握数形结合思想与方程思想的应用．