题目内容
18.已知二次函数y=-x2+(m-2)x+m+1.(1)试说明:无论m取何实数,这个二次函数的图象必与x轴有两个交点;
(2)当m为何值时,函数图象的对称轴是y轴?
(3)当m为何值时,函数图象与x轴的两个交点都在原点的左侧?
分析 (1)求得b2-4ac的值,再证明大于0即可;
(2)根据对称轴公式,使对称轴为0,求得m的值即可;
(3)设函数图象与x轴的两个交点的横坐标分别为x1,x2,根据根与系数的关系列出关于m的不等式组即可.
解答 解:(1)△=(m-2)2-4×(-1)(m+1)=m2+8>0,
∵m2≥0,
∴m2+8>0,
∴无论m为何实数,二次函数图象与x轴必有两个交点.
(2)∵-$\frac{b}{2a}$=-$\frac{m-2}{-2}$=0,
∴m=2;
(3)设二次函数图象与x轴的两个交点为(x1,0),(x2,0),
则$\left\{{\begin{array}{l}{{x_1}+{x_2}=m-2<0}\\{{x_1}{x_2}=-(m+1)>0}\end{array}}\right.$,
解得m<-1.
点评 本题考查了抛物线和x轴的交点问题,以及根与系数的关系,明确x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$是解题的关键.

练习册系列答案
相关题目
8.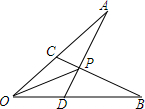 如图,OP平分∠AOB,且OA=OB.则图中全等的三角形为( )
如图,OP平分∠AOB,且OA=OB.则图中全等的三角形为( )
 如图,OP平分∠AOB,且OA=OB.则图中全等的三角形为( )
如图,OP平分∠AOB,且OA=OB.则图中全等的三角形为( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
6.在下列选项中,具有相反意义的量是( )
| A. | 收入20元与支出30元 | B. | 2个苹果和2个梨 | ||
| C. | 走了100米又跑了100米 | D. | 向东行30米和向北行30米 |
10.下列图形不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列运算正确的是( )
| A. | x3•x4=x12 | B. | (x3)4=x12 | C. | x6÷x2=x3 | D. | x3+x4=x7 |
