题目内容
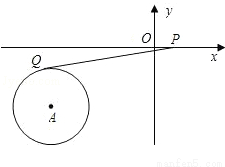
如图所示，在直角坐标系中，A点坐标（－3，－2），⊙A的半径为1，P为x轴上一动点，PQ切⊙A于点Q，则当PQ最小时，P点的坐标为（ ）
A．（－4，0） B．（－2，0） C．（－3，0） D．（－4，0）或（－2，0）
C．
【解析】
试题分析：连接AQ，AP．根据切线的性质定理，得AQ⊥PQ，要使PQ最小，只需AP最小，则根据垂线段最短，则作AP⊥x轴于P，即为所求作的点P，此时P点的坐标是（﹣3，0）．故选C．
考点：1．直线与圆的位置关系；2．坐标与图形性质．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
三角形的外心是（ ）
| A．各内角的平分线的交点 | B．各边中线的交点 |
| C．各边垂线的交点 | D．各边垂直平分线的交点 |
（
）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）
B．
C．
D．
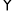ABCD中，AB=4，点D的坐标是（0，8），以点C为顶点的抛物线
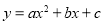经过x轴上的点A、B．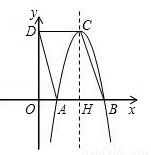
（
）经过A（-1，0）、B（3，0）两点，抛物线与y轴交点为C，其顶点为D，连接BD，点P是线段BD上一个动点（不与B，D重合），过点P作y轴的垂线，垂足为E，连接BE．
，
），△PBE的面积为
，求
与
的函数关系式，写出自变量
的取值范围.
的直径，弦
于点E，
，⊙O的半径为
，则弦
的长为____________