题目内容
(8分)
如图所示,在平面直角坐标系中,抛物线 (
( )经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
)经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.

(1)求抛物线的解析式,并写出顶点D的坐标;
(2)如果P点的坐标为( ,
, ),△PBE的面积为
),△PBE的面积为 ,求
,求 与
与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围.
的取值范围.
(1)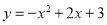 ,D(1,4);(2)
,D(1,4);(2)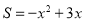 (
(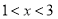 ).
).
【解析】
试题分析:(1)本题需先根据抛物线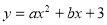
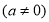 经过A(﹣1,0)、B(3,0)两点,分别求出a、b的值,再代入抛物线
经过A(﹣1,0)、B(3,0)两点,分别求出a、b的值,再代入抛物线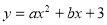 即可求出它的解析式.
即可求出它的解析式.
(2)本题首先设出BD解析式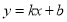 ,再把B、D两点坐标代入求出k、b的值,得出BD解析式,再根据面积公式即可求出最大值.
,再把B、D两点坐标代入求出k、b的值,得出BD解析式,再根据面积公式即可求出最大值.
试题解析:(1)∵抛物线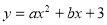 (
(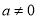 )经过A(﹣1,0)、B(3,0)两点∴把(﹣1,0)B(3,0)代入抛物线得:
)经过A(﹣1,0)、B(3,0)两点∴把(﹣1,0)B(3,0)代入抛物线得: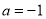 ,
,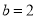 ,∴抛物线解析式为:
,∴抛物线解析式为: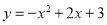 ,∵
,∵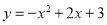 =
=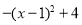 ,∴顶点D的坐标为(1,4);
,∴顶点D的坐标为(1,4);
(2)设直线BD解析式为: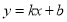 (
(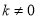 ),把B、D两点坐标代入,得:
),把B、D两点坐标代入,得: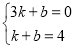 ,解得
,解得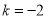 ,
,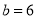 ,直线BD解析式为
,直线BD解析式为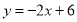 ,S=
,S=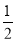 PE•OE=
PE•OE=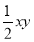 =
=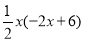 =
=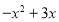 ,∵顶点D的坐标为(1,4),B(3,0)∴1<x<3.∴
,∵顶点D的坐标为(1,4),B(3,0)∴1<x<3.∴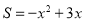 (
(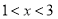 ).
).
考点:二次函数综合题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 的中点,过点M的弦MN交弦AB于点C,⊙O的半径为4cm,MN=4
的中点,过点M的弦MN交弦AB于点C,⊙O的半径为4cm,MN=4 cm.
cm.
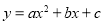 (
(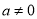 )的顶点坐标为(4,
)的顶点坐标为(4,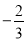 ),且与y轴交于点C(0,2),与x轴交于A、B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A、B两点(点A在点B的左边).
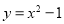 与x轴的交点个数是( )
与x轴的交点个数是( )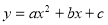 的图象如图所示,若
的图象如图所示,若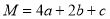 ,
,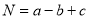 ,
,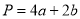 ,则( )
,则( )
 B.
B. C.
C. D.
D.
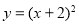 的图像沿y轴向上平移1个单位长度,与y轴的交点为C,则C点坐标是 .
的图像沿y轴向上平移1个单位长度,与y轴的交点为C,则C点坐标是 . 有两个不相等的实数根,则m的取值范围是( )
有两个不相等的实数根,则m的取值范围是( ) B.
B. C.
C. 且
且 D.
D.
