题目内容
如图，OC是∠AOD的平分线，OB是∠AOC的平分线，若∠COD=53°18′，则∠AOD=________，∠BOC=________．
106°36′ 26°39′
分析：首先根据角平分线的定义可得∠AOD=2∠COD，∠AOC=∠COD，∠BOC=
∠AOC，再根据∠COD=53°18′可算出答案．
解答：∵OC是∠AOD的平分线，
∴∠AOD=2∠COD，∠AOC=∠COD，
∵∠COD=53°18′，
∴∠AOD=2×53°18′=106°36′，∠AOC=53°18′，
∵OB是∠AOC的平分线，
∴∠BOC=∠AOC=
53°18′=26°39′，
故答案为：106°36′；26°39′．
点评：此题主要考查了角平分线定义，关键是掌握角平分线的定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．
分析：首先根据角平分线的定义可得∠AOD=2∠COD，∠AOC=∠COD，∠BOC=
∠AOC，再根据∠COD=53°18′可算出答案．解答：∵OC是∠AOD的平分线，
∴∠AOD=2∠COD，∠AOC=∠COD，
∵∠COD=53°18′，
∴∠AOD=2×53°18′=106°36′，∠AOC=53°18′，
∵OB是∠AOC的平分线，
∴∠BOC=
∠AOC=53°18′=26°39′，故答案为：106°36′；26°39′．
点评：此题主要考查了角平分线定义，关键是掌握角平分线的定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．
练习册系列答案
相关题目
如图，OC是∠AOD的平分线，OE是∠BOD的平分线．若∠AOB=130°，那么∠COE是多少度？
如图，OC是∠AOD的平分线，OE是∠BOD的平分线．
如图，OC是∠AOD的平分线，OB是∠AOC的平分线，若∠COD=53°18′，则∠AOD=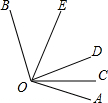
如图，OC是∠AOD的平分线，OE是∠DOB的平分线．
如图，OC是∠AOD的平分线，OE是∠BOD的平分线．