题目内容
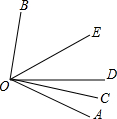 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线.(1)如果∠AOB=130°,那么∠COE是多少度;
(2)如果∠COD=20°,∠AOB=150°,那么∠BOE是多少度.
分析:(1)直接根据角平分线的定义进行解答即可;
(2)先根据∠COD=20°求出∠AOD的度数,再根据∠AOB=150°求出∠BOD的度数,根据角平分线的定义即可得出结论.
(2)先根据∠COD=20°求出∠AOD的度数,再根据∠AOB=150°求出∠BOD的度数,根据角平分线的定义即可得出结论.
解答:解:(1)∵OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130°
∴∠COE=
∠BOD+
∠AOD
=
(∠BOD+∠AOD)
=
∠AOB
=65°;
(2)∵∠COD=20°,
∴∠AOD=2×20°=40°,
∵∠AOB=150°,
∴∠BOD=∠AOB-∠AOD=150°-40°=110°,
∵OE是∠BOD的平分线,
∴∠BOE=
∠BOD=
×110°=55°.
∴∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=65°;
(2)∵∠COD=20°,
∴∠AOD=2×20°=40°,
∵∠AOB=150°,
∴∠BOD=∠AOB-∠AOD=150°-40°=110°,
∵OE是∠BOD的平分线,
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是角平分线的定义,熟知各角之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.若∠AOB=130°,那么∠COE是多少度?
如图,OC是∠AOD的平分线,OE是∠BOD的平分线.若∠AOB=130°,那么∠COE是多少度? 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线. 如图,OC是∠AOD的平分线,OB是∠AOC的平分线,若∠COD=53°18′,则∠AOD=
如图,OC是∠AOD的平分线,OB是∠AOC的平分线,若∠COD=53°18′,则∠AOD=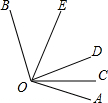 如图,OC是∠AOD的平分线,OE是∠DOB的平分线.
如图,OC是∠AOD的平分线,OE是∠DOB的平分线.