题目内容
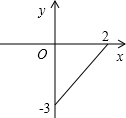 已知变量y与x的函数图象如图,则函数关系式为( )
已知变量y与x的函数图象如图,则函数关系式为( )A、y=-
| ||
B、y=-
| ||
C、y=
| ||
D、y=
|
考点:待定系数法求一次函数解析式
专题:
分析:根据图象可知y是x的一次函数,设函数解析式为y=kx+b,把(2,0),(0,-3)代入y=kx+b,运用待定系数法即可求出函数的解析式,然后根据图象确定x的取值范围.
解答:解:设y=kx+b.
∵图象经过点(2,0),(0,-3),
∴
,
解得
,
∴y=
x-3(0≤x≤2).
故选C.
∵图象经过点(2,0),(0,-3),
∴
|
解得
|
∴y=
| 3 |
| 2 |
故选C.
点评:考查了用待定系数法求一次函数的解析式.先设y=kx+b,再结合图象把已知点的坐标代入可求出k,b的值,即得一次函数的解析式.

练习册系列答案
相关题目
已知m、n互为相反数,c,d互为倒数,a到原点的距离为1,求3m+3n+2cd+a的值为( )
| A、3 | B、1 | C、3或1 | D、不能确定 |
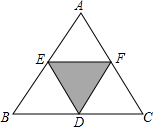 如图,是一名学生制作的劳技作品,他把△ABC各边中点连接得到△DEF与△ABC相似吗?为什么?
如图,是一名学生制作的劳技作品,他把△ABC各边中点连接得到△DEF与△ABC相似吗?为什么?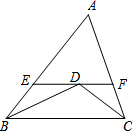 已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F.AB=8,AC=6,求三角形AEF的周长.
已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F.AB=8,AC=6,求三角形AEF的周长.