题目内容
若关于x的一元二次方程ax2+2(a+2)x+a=0有实数根,则a的取值范围是 .
考点:根的判别式,一元二次方程的定义
专题:
分析:由关于x的一元二次方程ax2+2(a+2)x+a=0有实数根及一元二次方程的定义,即可得判别式△≥0,a≠0,继而可求得a的范围.
解答:解:∵关于x的一元二次方程ax2+2(a+2)x+a=0有实数根,
∴△=b2-4ac=[2(a+2)]2-4×a×a=16a+16≥0,
解得:a≥-1,
∵方程ax2+2(a+2)x+a=0是一元二次方程,
∴a≠0,
∴a的范围是:a≥-1且a≠0.
故答案为a≥-1且a≠0.
∴△=b2-4ac=[2(a+2)]2-4×a×a=16a+16≥0,
解得:a≥-1,
∵方程ax2+2(a+2)x+a=0是一元二次方程,
∴a≠0,
∴a的范围是:a≥-1且a≠0.
故答案为a≥-1且a≠0.
点评:此题考查了一元二次方程判别式的知识.此题比较简单,注意掌握一元二次方程有两个实数根,即可得△≥0.同时考查了一元二次方程的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列计算结果正确的是( )
| A、2x+5y=7xy |
| B、2a2+2a3=4a5 |
| C、4a2-3a2=1 |
| D、-2a2b+a2b=-a2b |
下列图形中具有稳定性的是( )
A、 |
B、 |
C、 |
D、 |
 已知图中的两个三角形全等,则∠1等于( )
已知图中的两个三角形全等,则∠1等于( )| A、70° | B、68° |
| C、58° | D、52° |
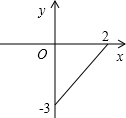 已知变量y与x的函数图象如图,则函数关系式为( )
已知变量y与x的函数图象如图,则函数关系式为( )A、y=-
| ||
B、y=-
| ||
C、y=
| ||
D、y=
|
 按图所示的程序计算,若开始输入的x值为1,则最后输出的结果是
按图所示的程序计算,若开始输入的x值为1,则最后输出的结果是