题目内容
二次函数与x轴的交点为（2，0）和（-6，0），且经过点（3，9），求这个函数的关系式 ．
考点：待定系数法求二次函数解析式
专题：
分析：根据题意设二次函数解析式为y=a（x+6）（x-2），把已知点（3，9）代入求出a的值，即可确定出解析式．
解答：解：设二次函数解析式为y=a（x+6）（x-2），
把x=3，y=9代入得：9=9a，即a=1，
则二次函数解析式为y=（x+6）（x-2）=x2+4x-12．
故答案为y=x2+4x-12．
把x=3，y=9代入得：9=9a，即a=1，
则二次函数解析式为y=（x+6）（x-2）=x2+4x-12．
故答案为y=x2+4x-12．
点评：此题考查了待定系数法求二次函数解析式，熟练掌握待定系数法是解本题的关键．
练习册系列答案
相关题目
已知一个多边形的内角和与外角和的比是9：2，则这个多边形的边数是（ ）
| A、9 | B、10 | C、11 | D、12 |
下列计算正确的是（ ）
A、
| ||||||||
B、
| ||||||||
C、5
| ||||||||
D、2
|
将一元一次方程3x2-1=6x化成一般形式后，二次项系数和一次项系数分别为（ ）
| A、3，-6 |
| B、3，6 |
| C、3，-1 |
| D、3x2，-6x |
下列计算结果正确的是（ ）
| A、2x+5y=7xy |
| B、2a2+2a3=4a5 |
| C、4a2-3a2=1 |
| D、-2a2b+a2b=-a2b |
下列运算正确的是（ ）
| A、4x2y-xy2=3x2y |
| B、3（x-1）=3x-1 |
| C、-3a+7a+1=-10a+1 |
| D、-（x-6）=-x+6 |
方程（x-4）（x+3）=0的根是（ ）
| A、x1=-4，x2=3 |
| B、x1=4，x2=3 |
| C、x1=4，x2=-3 |
| D、x1=-4，x2=-3 |
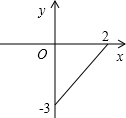已知变量y与x的函数图象如图，则函数关系式为（ ）A、y=-
| ||
B、y=-
| ||
C、y=
| ||
D、y=
|