题目内容
已知m、n互为相反数，c，d互为倒数，a到原点的距离为1，求3m+3n+2cd+a的值为（ ）
| A、3 | B、1 | C、3或1 | D、不能确定 |
考点：代数式求值,数轴,相反数,倒数
专题：计算题
分析：原式利用相反数，倒数，以及绝对值的代数意义求出m+n，cd以及a的值，代入原式计算即可得到结果．
解答：解：由题意得：m+n=0，cd=1，a=1或-1，
当a=1时，原式=3（m+n）+2cd+a=0+2+1=3；
当a=-1时，原式=3（m+n）+2cd+a=0+2-1=1，
故选C
当a=1时，原式=3（m+n）+2cd+a=0+2+1=3；
当a=-1时，原式=3（m+n）+2cd+a=0+2-1=1，
故选C
点评：此题考查了代数式求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
将一元一次方程3x2-1=6x化成一般形式后，二次项系数和一次项系数分别为（ ）
| A、3，-6 |
| B、3，6 |
| C、3，-1 |
| D、3x2，-6x |
三个正方形的面积如图所示，则正方形A的边长为（ ）| A、6 | B、8 | C、36 | D、64 |
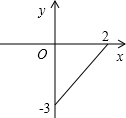已知变量y与x的函数图象如图，则函数关系式为（ ）A、y=-
| ||
B、y=-
| ||
C、y=
| ||
D、y=
|
用配方法解方程x2-2x-5=0时，原方程变形正确的是（ ）
| A、（x-1）2=6 |
| B、（x-2）2=9 |
| C、（x+1）2=6 |
| D、（x+2）2=9 |
在△ABC中，∠C=90°，CD⊥AB于点D，则直线AC与△BDC的外接圆的位置关系是（ ）
| A、相离 | B、相切 |
| C、相交 | D、无法确定 |