题目内容
6.计算(a2b)3=a6b3.(-a2)3+(-a3)2=0.3x3•(-2x2)=-6x5;(a2b )2=a4b2;(2n+4)2n-1=22n+3.
分析 根据积的乘方等于乘方的积,可得答案;
根据积的乘方等于乘方的积,可得同类项,根据合并同类项,可得答案;
根据单项式的乘法,系数乘以系数,同底数的幂相乘,可得答案;
根据积的乘方等于乘方的积,可得答案;
根据同底数幂的乘法底数不变指数相加,可得答案.
解答 解:(a2b)3=a6b3.
(-a2)3+(-a3)2=0.
3x3•(-2x2)=-6x5;
( a2b )2=a4b2;
( 2n+4)2n-1=22n+3.
故答案为:a6b3,0,-6x5,a2b,2n+4.
点评 本题考查了单项式乘单项式,熟记法则并根据法则计算是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列计算正确的是( )
| A. | (6a9)÷(3a3)=2a3 | B. | (-4x3y)÷(2x2y)=-2x | C. | (x-y)3÷(y-x)=(y一x)2 | D. | am÷an÷ap=am-n+p |
11.下列说法正确的是( )
| A. | 2π是偶数 | B. | $\frac{31}{13}$是无理数 | ||
| C. | $\frac{\sqrt{3}}{2}$是分数 | D. | $\root{3}{25}$是无限不循环小数 |
18.下列各式中正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{-16}$=-4 | C. | (-$\sqrt{3}$)2=9 | D. | $\sqrt{(-5)^{2}}$=5 |
15.计算(-m2)3•m4的结果等于( )
| A. | -m9 | B. | m9 | C. | -m10 | D. | m8 |
16.已知△ABC的三边长分别为a,b,c,且满足(a-5)2+|b-12|+$\sqrt{c-13}$=0,则△ABC( )
| A. | 不是直角三角形 | B. | 是以a为斜边的直角三角形 | ||
| C. | 是以b为斜边的直角三角形 | D. | 是以c为斜边的直角三角形 |
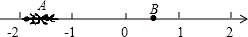 如图所示,一只蚂蚁从点A沿数轴向右爬2个单位到达点B,点A表示$-\sqrt{2}$,设点B所表示的数为m,则|m-1|的值是1-m.
如图所示,一只蚂蚁从点A沿数轴向右爬2个单位到达点B,点A表示$-\sqrt{2}$,设点B所表示的数为m,则|m-1|的值是1-m.