��Ŀ����
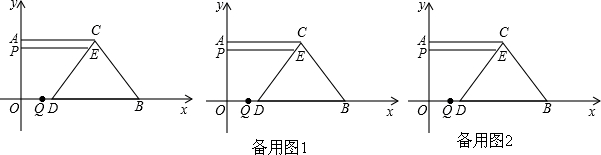
��ͼ��ֱ������AOBC��ƽ��ֱ������ϵ�У�AO=4��AC=5��OB=8��D��OB�ϣ���OD=2����CD��������������P��Q�ֱ�ӵ�A�͵�Oͬʱ���������е�P��1/s���ٶȣ���AO���յ�O�ƶ�����Q��2/s���ٶ���OB���յ�B�ƶ�������P��PE��AC��CD�ڵ�E���趯���˶�ʱ��Ϊt�룮
��1����CD�ij�������t�Ĵ���ʽ��ʾDE��
��2����tΪ��ֵʱ������P��E��Q��DΪ������ı�����ƽ���ı��Σ�����P��E��Q��BΪ������ı�����ƽ���ı��Σ�ע��ֻ��Ӣ٣�������ѡһ�ֽ��м��㣩�����������ѡƽ���ı��ε������
��3����tΪ��ֵʱ����EDQΪֱ�������Σ�
��1����CD�ij�������t�Ĵ���ʽ��ʾDE��
��2����tΪ��ֵʱ������P��E��Q��DΪ������ı�����ƽ���ı��Σ�����P��E��Q��BΪ������ı�����ƽ���ı��Σ�ע��ֻ��Ӣ٣�������ѡһ�ֽ��м��㣩�����������ѡƽ���ı��ε������
��3����tΪ��ֵʱ����EDQΪֱ�������Σ�

���㣺�ı����ۺ���
ר�⣺ѹ����
��������1����CF��OB��F��EG��OB��G���ɹ��ɶ����Ϳ������CD��ֵ���Ϳ������sin��CDF��ֵ�������Ǻ���ֵ�Ϳ��Ա�ʾ��DE��
��2���ٵ��ı���PEQD��ƽ���ı���ʱ���������ھͿ��Եó�PE=DQ�����������ʽ������������⼴�ɣ��ڵ��ı���ACBQΪƽ���ı���ʱ����PE=BQ�������������⼴�ɣ�
��3����������ۣ�����EQD=90��ʱ����ͼ2�ɹ��ɶ���������4-t��2+��2t-2��2=��5-
t��2�Ϳ���������ۣ�
����DEQ=90��ʱ����ͼ3�������EQ=
�����ɹ��ɶ������÷��̣�2t-2��2=��5-
t��2+��
��2�������⼴�ɣ�
��2���ٵ��ı���PEQD��ƽ���ı���ʱ���������ھͿ��Եó�PE=DQ�����������ʽ������������⼴�ɣ��ڵ��ı���ACBQΪƽ���ı���ʱ����PE=BQ�������������⼴�ɣ�
��3����������ۣ�����EQD=90��ʱ����ͼ2�ɹ��ɶ���������4-t��2+��2t-2��2=��5-
| 5 |
| 4 |
����DEQ=90��ʱ����ͼ3�������EQ=
| 8t-8 |
| 5 |
| 5 |
| 4 |
| 8t-8 |
| 5 |
����⣺��1����CF��OB��F��EG��OB��G��
���EGD=��CFD=90�㣮
��AC��OB����AOB=90�㣬
���CAO=90�㣬
���CAO=��AOB=��CFO=90�㣬
���ı���AOFC�Ǿ��Σ�
��AO=CF��AC=OF��
��AC=5��OA=4
��OF=5��CF=4
��OD=2��
��DF=3��
��Rt��DFC�У��й��ɶ�������
CD=5��
��sin��CDB=
��tan��CDF=
��sin��EDG=
��EG��OB��AO��OB��
��AO��EG����EGO=90�㣮
��PE��OB��
���ı���POGE�Ǿ��Σ�
��OP=EG��
��OA=4��AP=t��
��OP=4-t��
��EG=4-t
��
=
��
��
=
��
��DE=5-
t��
��CD=5��DE=5-
t��
��2���١��ı���PEQD��ƽ���ı��Σ�
��PE=DQ��
��EG=4-t��tan��CDF=
��
��
=
��
��
=
��
��DG=3-
t��
��PE=2+3-
t=5-
t��
��OQ=2t��
��DQ=2t-2��
��2t-2=5-
t��
��t=
��
��DQ=2��
-2=
��EG=4-
=
��
��S=
��
=
��
�ڡ��ı���PEQB��ƽ���ı��Σ�
��PE=QB��
��QB=OB-OQ=8-2t
��8-2t=5-
t��
��t=
��
��EG=4-
=
��QB=8-2��
=
��
��S=
��
=
��
��3���ٵ���EQD=90��ʱ����ͼ2
�ɹ��ɶ�������
��4-t��2+��2t-2��2=��5-
t��2��
��ã�t1=
��t2=-
����ȥ����
�ڵ���DEQ=90��ʱ����ͼ3��
��DF=OF-OD=5-
t-2=3-
t��
��sin��EDQ=
=
��
��EQ=
�ɹ��ɶ�������
��2t-2��2=��5-
t��2+��
��2��
49t2-3848t+9424=0��
��ã�t1=
��t2=76����ȥ����
�ۡ�EDQ��������ֱ�ǣ����Բ����ڣ�
t=
��=
ʱ����EDQΪֱ�������Σ�
���EGD=��CFD=90�㣮
��AC��OB����AOB=90�㣬
���CAO=90�㣬
���CAO=��AOB=��CFO=90�㣬
���ı���AOFC�Ǿ��Σ�
��AO=CF��AC=OF��
��AC=5��OA=4
��OF=5��CF=4
��OD=2��
��DF=3��
��Rt��DFC�У��й��ɶ�������
CD=5��
��sin��CDB=
| 4 |
| 5 |
| 4 |
| 3 |
��sin��EDG=
| 4 |
| 5 |
��EG��OB��AO��OB��
��AO��EG����EGO=90�㣮
��PE��OB��
���ı���POGE�Ǿ��Σ�
��OP=EG��
��OA=4��AP=t��
��OP=4-t��
��EG=4-t
��
| EG |
| ED |
| 4 |
| 5 |
��
| 4-t |
| ED |
| 4 |
| 5 |
��DE=5-
| 5 |
| 4 |
��CD=5��DE=5-
| 5 |
| 4 |
��2���١��ı���PEQD��ƽ���ı��Σ�

��PE=DQ��
��EG=4-t��tan��CDF=
| 4 |
| 3 |
��
| EG |
| DG |
| 4 |
| 3 |
��
| 4-t |
| DG |
| 4 |
| 3 |
��DG=3-
| 3 |
| 4 |
��PE=2+3-
| 3 |
| 4 |
| 3 |
| 4 |
��OQ=2t��
��DQ=2t-2��
��2t-2=5-
| 3 |
| 4 |
��t=
| 28 |
| 11 |
��DQ=2��
| 28 |
| 11 |
| 34 |
| 11 |
| 28 |
| 11 |
| 16 |
| 11 |
��S=
| 34 |
| 11 |
| 16 |
| 11 |
| 544 |
| 121 |
�ڡ��ı���PEQB��ƽ���ı��Σ�
��PE=QB��

��QB=OB-OQ=8-2t
��8-2t=5-
| 3 |
| 4 |
��t=
| 12 |
| 5 |
��EG=4-
| 12 |
| 5 |
| 8 |
| 5 |
| 12 |
| 5 |
| 16 |
| 5 |
��S=
| 8 |
| 5 |
| 16 |
| 5 |
| 128 |
| 25 |
��3���ٵ���EQD=90��ʱ����ͼ2
�ɹ��ɶ�������
��4-t��2+��2t-2��2=��5-
| 5 |
| 4 |

��ã�t1=
| 20 |
| 11 |
| 4 |
| 5 |
�ڵ���DEQ=90��ʱ����ͼ3��
��DF=OF-OD=5-
| 3 |
| 4 |
| 3 |
| 4 |
��sin��EDQ=
| EQ |
| DQ |
| 4 |
| 5 |
��EQ=
| 8t-8 |
| 5 |
�ɹ��ɶ�������
��2t-2��2=��5-
| 5 |
| 4 |
| 8t-8 |
| 5 |
49t2-3848t+9424=0��
��ã�t1=
| 124 |
| 49 |
�ۡ�EDQ��������ֱ�ǣ����Բ����ڣ�
t=
| 124 |
| 49 |
| 20 |
| 11 |
���������⿼�������ε����ʵ����ã�������Ǻ���ֵ�����ã�ֱ�������ε����ʵ����ã�ƽ���ı��ε����ʵ����ã����ɶ��������ã�ƽ���ı��ε���������ã����ʱ����������ʱ�亯��ֵ����ǹؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
���и�ʽ����ƽ���ʽ������ǣ�������
| A����2a+b����2b-a�� | ||||
B����-
| ||||
| C����a+b����a-2b�� | ||||
| D����2x-1����-2x+1�� |
 ��ͼ����֪ABΪ��O��ֱ����E��AB�ӳ�����һ�㣬��C�ǡ�O�ϵ�һ�㣬����EC��BC��AC���ҡ�BCE=��BAC��
��ͼ����֪ABΪ��O��ֱ����E��AB�ӳ�����һ�㣬��C�ǡ�O�ϵ�һ�㣬����EC��BC��AC���ҡ�BCE=��BAC��
 ��ͼ���ı���ABCD�Ǿ��Σ��Ѿ�����ֱ��BD�۵�����C���ڵ�E��������BE����AD���ڵ�M��
��ͼ���ı���ABCD�Ǿ��Σ��Ѿ�����ֱ��BD�۵�����C���ڵ�E��������BE����AD���ڵ�M��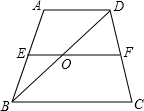 ��ͼ��������ABCD�У�AD��BC����E��AB�ϣ���F��CD�ϣ�EFΪ��λ�ߣ�EF��BD���ڵ�O����FO-EO=5����BC-AD=
��ͼ��������ABCD�У�AD��BC����E��AB�ϣ���F��CD�ϣ�EFΪ��λ�ߣ�EF��BD���ڵ�O����FO-EO=5����BC-AD=