题目内容
如图，AB与⊙O相切于点C，OA=OB，⊙O的半径为3cm，AB=8cm，则OA=（ ）| A、3cm | B、4cm |
| C、5cm | D、6cm |
考点：切线的性质
专题：
分析：连接OC，AB为切线，所以有OC⊥AB，根据题意，得C为△AOB的中点，即AC=4cm，根据勾股定理即可得出OA的长度．
解答：
解：连接OC；
∵AB与⊙O相切于点C，
∴OC⊥AB，
∵OA=OB，
∴AC=BC=4cm，
在Rt△AOC中，
OA=
=
=5（cm）．
故选C．
解：连接OC；∵AB与⊙O相切于点C，
∴OC⊥AB，
∵OA=OB，
∴AC=BC=4cm，
在Rt△AOC中，
OA=
| AC2+OC2 |
| 42+32 |
故选C．
点评：本题考查了切线与圆的位置关系，利用勾股定理求解直角三角形的知识．
练习册系列答案
相关题目
如图所示的几何体的三种视图是（ ）A、 |
B、 |
C、 |
D、 |
如图，△ABC中，AE⊥BC于E，D为AB边上一点，如果BD=2AD，CD=10，sin∠BCD=
如图，在如图网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠AOB的正切值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个正方体的六个面上分别标有-1，-2，-3，-4，-5，-6中的一个数，各个面上所标数字都不相同，如图是这个正方体的三种放置方法，三个正方体下底面所标数字分别是a，b，c，则a+b+c+abc= ．
在有理数：-9、8.7、-
、2006、-6.1、0、-
中，负数有（ ）个．
| 2 |
| 5 |
| 1 |
| 3 |
| A、2 | B、3 | C、4 | D、5 |
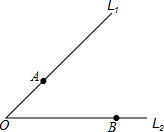如图，由同一点O出发的两公交车分别沿道路L1、L2行驶且两公路分别经过A、B两个小区门口．