题目内容
7. 如图,将△AOB绕点O逆时针方向旋转90°,得到△A′OB′,看点A的坐标为(2,1),则点A′坐标为(-1,2).
如图,将△AOB绕点O逆时针方向旋转90°,得到△A′OB′,看点A的坐标为(2,1),则点A′坐标为(-1,2).
分析 利用旋转的性质得OB′=OB=2,A′B′=AB=1,∠BOB′=90°,∠OB′A′=∠OBA=90°,然后利用第二象限内点的坐标特征写出点A′坐标.
解答 解:∵A(2,1),
∴AB=1,OB=2,
∵△AOB绕点O逆时针方向旋转90°,得到△A′OB′,
∴OB′=OB=2,A′B′=AB=1,∠BOB′=90°,∠OB′A′=∠OBA=90°,
∴点A′坐标为(-1,2).
故答案为(-1,2).
点评 本题考查了坐标与图形变化:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
相关题目
17.一个等腰三角形有两边长分别为2cm、5cm,那么它的周长是( )
| A. | 9cm | B. | 9cm或12cm | C. | 12cm | D. | 无法确定 |
15. 如图,要使△ACD∽△ABC只需添加的条件是( )
如图,要使△ACD∽△ABC只需添加的条件是( )
 如图,要使△ACD∽△ABC只需添加的条件是( )
如图,要使△ACD∽△ABC只需添加的条件是( )| A. | ∠ADC=∠B | B. | AC2=AD•AB | C. | $\frac{BC}{CD}=\frac{CA}{DA}$ | D. | $\frac{AC}{AB}=\frac{CD}{BC}$ |
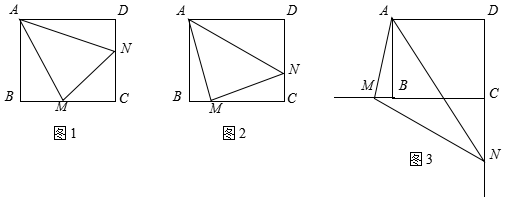
 如图,在矩形ABCD中,AB=8,AD=6,动点E从点C出发,以每秒1个单位长度的速度沿CD方向匀速运动,与此同时,动点F从点A出发,以每秒2个单位长度的速度沿对角线AC方向匀速运动,当点F到达点C时,E,F两点同时停止运动,连结EF,设运动时间为t秒.
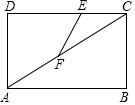
如图,在矩形ABCD中,AB=8,AD=6,动点E从点C出发,以每秒1个单位长度的速度沿CD方向匀速运动,与此同时,动点F从点A出发,以每秒2个单位长度的速度沿对角线AC方向匀速运动,当点F到达点C时,E,F两点同时停止运动,连结EF,设运动时间为t秒. 如图,正方形ABCD中,E与F分别是AD、BC上一点,∠1=∠2.
如图,正方形ABCD中,E与F分别是AD、BC上一点,∠1=∠2.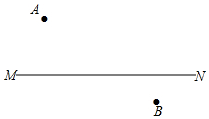 如图,在直线MN的异侧有A、B两点,按要求画图取点,并写出画图的依据.
如图,在直线MN的异侧有A、B两点,按要求画图取点,并写出画图的依据.