题目内容
15. 如图,要使△ACD∽△ABC只需添加的条件是( )
如图,要使△ACD∽△ABC只需添加的条件是( )| A. | ∠ADC=∠B | B. | AC2=AD•AB | C. | $\frac{BC}{CD}=\frac{CA}{DA}$ | D. | $\frac{AC}{AB}=\frac{CD}{BC}$ |
分析 由于△ACD和△ABC有一个公共角,则利用有两组角对应相等的两个三角形相似可对A进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对B、C、D进行判断.
解答 解:∵∠DAC=∠CAB,
∴当∠ADC=∠ACB时,△ACD∽△ABC;
当∠ACD=∠B时,△ACD∽△ABC;
当$\frac{AD}{AC}$=$\frac{AC}{AB}$时,即AC2=AD•AB,△ACD∽△ABC.
故选B.
点评 本题考查了相似三角形的判定:灵活掌握相似三角形的判定方法.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
6.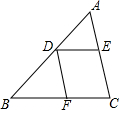 如图,在△ABC中,D是AB边上一点,DE∥BC,DF∥AC,下列结论正确的是( )
如图,在△ABC中,D是AB边上一点,DE∥BC,DF∥AC,下列结论正确的是( )
 如图,在△ABC中,D是AB边上一点,DE∥BC,DF∥AC,下列结论正确的是( )
如图,在△ABC中,D是AB边上一点,DE∥BC,DF∥AC,下列结论正确的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{AC}$ | B. | $\frac{DE}{BF}$=$\frac{AE}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{AD}{BD}$=$\frac{DF}{AC}$ |
3.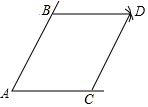 如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD.则根据作图过程判定四边形ABDC是菱形的依据是( )
如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD.则根据作图过程判定四边形ABDC是菱形的依据是( )
 如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD.则根据作图过程判定四边形ABDC是菱形的依据是( )
如图,点B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD.则根据作图过程判定四边形ABDC是菱形的依据是( )| A. | 一组邻边相等的四边形是菱形 | |
| B. | 四边相等的四边形是菱形 | |
| C. | 对角线互相垂直的平行四边形是菱形 | |
| D. | 对角线平分一组对角的四边形是菱形 |
5.以下列各组线段长为边,能组成三角形的是( )
| A. | 1cm,2cm,4cm | B. | 8cm,6cm,4cm | C. | 12cm,5cm,6cm | D. | 2cm,3cm,6cm |
 如图,将△AOB绕点O逆时针方向旋转90°,得到△A′OB′,看点A的坐标为(2,1),则点A′坐标为(-1,2).
如图,将△AOB绕点O逆时针方向旋转90°,得到△A′OB′,看点A的坐标为(2,1),则点A′坐标为(-1,2).