题目内容
16．
如图，正方形ABCD中，E与F分别是AD、BC上一点，∠1=∠2．求证：BE=DF．
分析 由∠1=∠2，可得BE∥DF，再由正方形的性质可得四边形EDFB为平行四边形，由平行四边形的性质即可证明BE=DF．
解答 证明：
∵四边形ABCD是正方形，
∴AD∥BC，
∵∠1=∠EBC，∠1=∠2，
∴∠2=∠EBC，
∴BE∥DF，
又∵AD∥BC，
∴四边形BEDF为平行四边形，
∴BE=DF．
点评 本题考查了正方形的性质，平行线的性质以及平行四边形的判断和性质，熟练特殊四边形的各种判断方法和各种性质是解题关键．
练习册系列答案
相关题目
6．
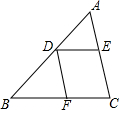如图，在△ABC中，D是AB边上一点，DE∥BC，DF∥AC，下列结论正确的是（ ）
如图，在△ABC中，D是AB边上一点，DE∥BC，DF∥AC，下列结论正确的是（ ）| A． | $\frac{AD}{BD}$=$\frac{AE}{AC}$ | B． | $\frac{DE}{BF}$=$\frac{AE}{AC}$ | C． | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D． | $\frac{AD}{BD}$=$\frac{DF}{AC}$ |
如图，将△AOB绕点O逆时针方向旋转90°，得到△A′OB′，看点A的坐标为（2，1），则点A′坐标为（-1，2）．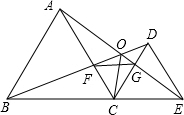
如图，已知△ABC和△DCE均是等边三角形，点B、C、E在同一条直线上，AE与BD交于点O，AE与CD交于点G，AC与BD交于点F，连接OC、FG，则下列结论：①AE=BD；②AO=BF；③FG∥BE；④∠BOC=∠EOC；⑤BO=OC+AO，其中正确的结论有（ ）个．
已知有理数a，b，c在数轴上的位置如图所示，|a|=4，|c|=1，按要求完成下列各小题．
5．以下列各组线段长为边，能组成三角形的是（ ）
| A． | 1cm，2cm，4cm | B． | 8cm，6cm，4cm | C． | 12cm，5cm，6cm | D． | 2cm，3cm，6cm |