题目内容
4. 如图所示,设I是△ABC的内心(三条角平分线的交点),AI的延长线交BC边于点D,交△ABC的外接圆于点E,若IE=4,AE=8,则线段DE的长是2.
如图所示,设I是△ABC的内心(三条角平分线的交点),AI的延长线交BC边于点D,交△ABC的外接圆于点E,若IE=4,AE=8,则线段DE的长是2.
分析 根据题意可以得到△BED和△AEB相似的条件,然后根据相似三角形对应边成比例,可以求得DE的长,从而可以解答本题.
解答 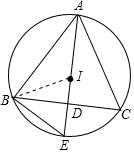 解:连接IB,如右图所示,
解:连接IB,如右图所示,
∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠IBD,
又∵∠BIE=∠BAD+∠ABI=∠CAD+∠IBD=∠IBD+∠DBE=∠IBE,
∴BE=IE,
在△BED和△AEB中,
∠EBD=∠CAD=∠BAD,∠BED=∠AEB,
∴△BED∽△AEB,
∴$\frac{BE}{AE}=\frac{DE}{BE}$,
∵IE=4,AE=8,
∴BE=4,
即DE=$\frac{B{E}^{2}}{AE}=\frac{{4}^{2}}{8}=2$,
故答案为:2.
点评 本题考查三角形的内心与外心、三角形相似,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列比较大小正确的是( )
| A. | -(-21)<+(-21) | B. | -|-10$\frac{1}{2}$|>8$\frac{2}{3}$ | C. | -|-7|=-(-7$\frac{2}{3}$) | D. | -$\frac{5}{6}$<-$\frac{4}{5}$ |
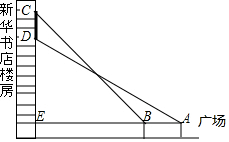 如图,小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6m到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21m,则该屏幕上端与下端之间的距离CD为(21-9$\sqrt{3}$)m.
如图,小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6m到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21m,则该屏幕上端与下端之间的距离CD为(21-9$\sqrt{3}$)m. 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是多少?
在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是多少? 如图所示,在两个直角三角形中,∠ACB=∠ADC=90°,AC=$\sqrt{6}$,AD=2,CD=$\sqrt{2}$,当AB的长度为多少时,这两个直角三角形相似?
如图所示,在两个直角三角形中,∠ACB=∠ADC=90°,AC=$\sqrt{6}$,AD=2,CD=$\sqrt{2}$,当AB的长度为多少时,这两个直角三角形相似?