题目内容
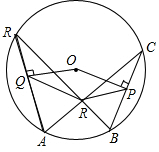 如图,已知AC、BD是⊙O的两条相互垂直的弦,并且AC、BD相交于点R,OP⊥BC,OQ⊥AD.求证:四边形OPRQ为平行四边形.
如图,已知AC、BD是⊙O的两条相互垂直的弦,并且AC、BD相交于点R,OP⊥BC,OQ⊥AD.求证:四边形OPRQ为平行四边形.考点:平行四边形的判定,三角形中位线定理,圆周角定理
专题:证明题
分析:连接BO并延长交圆O于E,连接CE,根据BE是直径,得到∠BCE=90°,然后根据∠ACB+∠ACE=90°,∠ADB+∠CAD=90°,∠ADB=∠ACB得到∠ACE=∠CAD,从而得到
=
,利用等弧对等弦德尔AD=CE然后根据中位线定理得到PO=
CE和根据直角三角形的性质得到RQ=
AD,从而得到PO=RQ 同理,连接AO并延长,交圆O于F,连接DF,同样可证得RP=OQ,从而判定四边形OPRQ为平行四边形.
 |
| AD |
 |
| CE |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: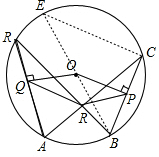 连接BO并延长交圆O于E,连接CE,
连接BO并延长交圆O于E,连接CE,
∵BE是直径,
∴∠BCE=90°
∵∠ACB+∠ACE=90°,∠ADB+∠CAD=90°,∠ADB=∠ACB﹙等弧﹚
∴∠ACE=∠CAD
∴
=
∴AD=CE
∵PO=
CE﹙中位线﹚,RQ=
AD﹙直角三角形斜边上的中线﹚
∴PO=RQ ①
同理,连接AO并延长,交圆O于F,连接DF,
同样可证得RP=OQ ②
∴四边形OPRQ为平行四边形.
 连接BO并延长交圆O于E,连接CE,
连接BO并延长交圆O于E,连接CE,∵BE是直径,
∴∠BCE=90°
∵∠ACB+∠ACE=90°,∠ADB+∠CAD=90°,∠ADB=∠ACB﹙等弧﹚
∴∠ACE=∠CAD
∴
 |
| AD |
 |
| CE |
∴AD=CE
∵PO=
| 1 |
| 2 |
| 1 |
| 2 |
∴PO=RQ ①
同理,连接AO并延长,交圆O于F,连接DF,
同样可证得RP=OQ ②
∴四边形OPRQ为平行四边形.
点评:本题考查了平行四边形的性质、三角形的中位线定理及圆周角定理,解题的关键是正确的作出辅助线,难度不大.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 如图所示,拦水坝横截面为等腰梯形ABCD,背水坡AB坡度为
如图所示,拦水坝横截面为等腰梯形ABCD,背水坡AB坡度为 如图,已知△ABC,根据题意完成下列各题:
如图,已知△ABC,根据题意完成下列各题: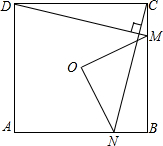 如图,O是正方形ABCD的中心,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM,交AB于点N,连接OM、ON.求证:
如图,O是正方形ABCD的中心,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM,交AB于点N,连接OM、ON.求证: