题目内容
12.先化简,再求值:(x-1-$\frac{3}{x+1}$)÷$\frac{{x}^{2}+4x+4}{x+1}$,其中x是方程x2+x=2的解.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出方程的解得到x的值,代入计算即可求出值.
解答 解:原式=$\frac{(x+1)(x-1)-3}{x+1}$•$\frac{x+1}{(x+2)^{2}}$=$\frac{(x+2)(x-2)}{(x+2)^{2}}$=$\frac{x-2}{x+2}$,
解方程x2+x=2得:x1=1,x2=2,
当x=1时,原式=-$\frac{1}{3}$;当x=-2时,分式方程无意义.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.对于任意实数a、b,定义f(a,b)=a2+5a-b,如:f(2,3)=22+5×2-3,若f(x,2)=4,则实数x的值是( )
| A. | 1或-6 | B. | -1或6 | C. | -5或1 | D. | 5或-1 |
3.厦门市2014年中考体育考试中,某校九年级(3)班50人参加考试,具体的成绩与人数如表,则该班的中考体育的平均成绩是23.6分.
| 成绩 | 人数 |
| 25 | 24 |
| 24 | 10 |
| 22 | 10 |
| 20 | 6 |
17.函数y=$\frac{1}{2x-4}$中,自变量x的取值范围是( )
| A. | x≠2 | B. | x>2 | C. | x<2 | D. | x≠4 |
1.2013年11月7日杭州青年时报A05版以“杭州雾霾天数突破历史最高数据”为题报道了杭州市雾霾情况,并刊登了2004年至2012年全年的雾霾天数变化情况,如图所示,其中2013年的雾霾天数截止到10月份.根据下表,以下说法不正确的是( )
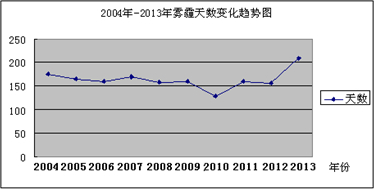

| A. | 2004年至2013年雾霾天数最少的是2010年 | |
| B. | 2012年到2013年雾霾天数上升明显 | |
| C. | 2004年至2012年雾霾天数呈下降趋势 | |
| D. | 2013年1-10月雾霾天数已超200天,可见环境污染越来越严重 |
2.观察数表:
根据数表排列的规律,第n行从右向左数的第5个数是n2+2n-4. (用正整数n表示)
| 第1行 | 1 2 3 |
| 第2行 | 4 5 6 7 8 |
| 第3行 | 9 10 11 12 13 14 15 |
| 第4行 | 16 17 18 19 20 21 22 23 24 |
| … | … |

 如图,在平面直角坐标系xOy中,点A(0,3),点B(4,3).
如图,在平面直角坐标系xOy中,点A(0,3),点B(4,3).