Question

12．已知A（2，0），B（0，2），在x轴上确定点M，使三角形MAB是等腰三角形，则M点的坐标为（0，0）（任写一个）．

Answer 1

分析 ①画AB的垂直平分线交x轴于一点；
②以A为圆心，AB长为半径交x轴于两点；
③以B为圆心，AB长为半径交交x轴于一点，再分别写出坐标即可．

解答 解：如图所示：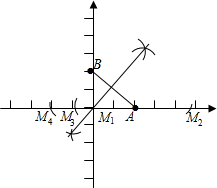
M₁（0，0），M₄（-2，0），
∵A（2，0），B（0，2），
∴AB=$\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2}$，
∵M₂，M₃是以A为圆心，AB长为半径交x轴于两点，
∴M₂（2+2$\sqrt{2}$，0），M₃（-2$\sqrt{2}$+2，0）．
故所有满足条件点M的坐标是：（0，0）（-2，0）（2+2$\sqrt{2}$，0），（-2$\sqrt{2}$+2，0）．

点评 此题主要考查了等腰三角形的判定与性质．注意分类讨论与数形结合思想的应用是解此题的关键．