题目内容
10.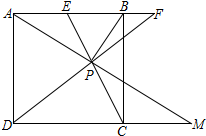 如图,点P为正方形ABCD内一点,且∠APB=90°,延长AP交直线CD于M,分别延长CP、DP交直线AB于点E、F
如图,点P为正方形ABCD内一点,且∠APB=90°,延长AP交直线CD于M,分别延长CP、DP交直线AB于点E、F(1)求证:$\frac{AE}{CM}$=$\frac{AF}{DM}$;
(2)求证:EF2=AF•BE;
(3)若E为AB的中点,直接写出tan∠APD的值.
分析 (1)因为AF∥DM,所以△AEP∽△MCP,△AFP∽△MDP,利用对应边的比相等可得$\frac{AE}{CM}=\frac{AP}{PM}=\frac{AF}{DM}$;
(2)延长BP交CD于点N,因为AF∥DM,类似(1)问中,易证$\frac{EF}{BE}$=$\frac{CD}{CN}$和$\frac{AF}{EF}$=$\frac{DM}{CD}$,再证明△BNC∽△MAD,利用正方形四边形相等即可得出$\frac{CN}{CD}=\frac{CD}{DM}$,从而得出EF2=AF•BE;
解答 (1)在正方形ABCD中,
AF∥DM,
∴△AEP∽△MCP,△AFP∽△MDP
∴$\frac{AE}{CM}$=$\frac{AP}{PM}$,$\frac{AP}{PM}$=$\frac{AF}{PM}$,
∴$\frac{AE}{CM}=\frac{AP}{PM}=\frac{AF}{DM}$,
∴$\frac{AE}{CM}$=$\frac{AF}{DM}$,
(2)延长BP交CD于点N,
∵EF∥CD,
∴△EFP∽△CDP,
∴$\frac{EF}{CD}$=$\frac{PE}{PC}$,
∵BE∥CN,
∴△EBP∽△CNP,
∴$\frac{BE}{CN}$=$\frac{PE}{PC}$,
∴$\frac{EF}{CD}=\frac{BE}{CN}$,
即$\frac{EF}{BE}$=$\frac{CD}{CN}$,
同理可证:$\frac{AF}{DM}$=$\frac{PF}{PD}$,$\frac{EF}{CD}$=$\frac{PF}{PD}$,
∴$\frac{AF}{DM}$=$\frac{EF}{CD}$,
即$\frac{AF}{EF}$=$\frac{DM}{CD}$,
∵∠APB=∠BPM=BCM=90°,
∴∠NBC=∠AMD,
∴△BNC∽△MAD,
∴$\frac{CN}{BC}$=$\frac{AD}{DM}$
∵AD=BC=CD,
∴$\frac{CN}{CD}=\frac{CD}{DM}$,
∴$\frac{EF}{BE}=\frac{AF}{EF}$,
∴EF2=AF•BE; (3)连接AN
(3)连接AN
由(2)可知,∠PNM=∠DAM,
∴A、P、N、D四点共圆,
∴∠APD=∠AND,
设BF=x,AB=2,
由(2)可知:EF2=AF•BE,
∴(1+x)2=(2+x),
∴x=-$\frac{1}{2}$±$\frac{\sqrt{5}}{2}$,
∵x>0,
∴x=$\frac{\sqrt{5}-1}{2}$,
∵$\frac{BF}{DN}=\frac{BP}{PN}=\frac{EB}{CN}$,
∴$\frac{BF}{DN}=\frac{EB}{CD-DN}$,
∴DN=3-$\sqrt{5}$,
∴在Rt△ADN中,
tan∠AND=$\frac{AD}{DN}$=$\frac{2}{3-\sqrt{5}}$=$\frac{{3+\sqrt{5}}}{2}$,
∴tan∠APD=tan∠AND=$\frac{3+\sqrt{3}}{2}$.
点评 本题考查相似三角形的性质与判定,涉及正方形的性质,锐角三角函数,相似三角形的性质等知识,题目较综合,需要学生灵活运用对应边的比相等进行求证,解题的关键是利用AF∥DM得出相似三角形.

| A. | 0.618 | B. | 0..618 | C. | 0.00618 | D. | 0.000618 |
| A. | x4 | B. | x3 | C. | 2x3 | D. | 2x4 |
 在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3).
在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3).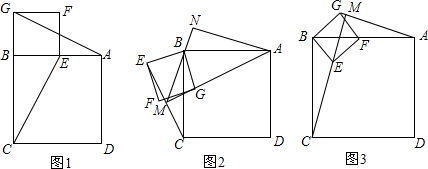
 对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如,下图中的函数有0,1两个不变值,其不变长度q等于1.
对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如,下图中的函数有0,1两个不变值,其不变长度q等于1. 如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.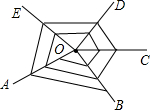 如图所示,以O为端点画5条射线OA,OB,OC,OD,OE后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2016个点在射线OA上.
如图所示,以O为端点画5条射线OA,OB,OC,OD,OE后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2016个点在射线OA上.