题目内容
19. 阅读:
阅读:我们知道,|a|=$\left\{\begin{array}{l}{a,a≥0}\\{-a,a<0}\end{array}\right.$于是要解不等式|x-3|≤4,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
解:(1)当x-3≥0,即x≥3时:x-3≤4
解这个不等式,得:x≤7
由条件x≥3,有:3≤x≤7
(2)当x-3<0,即 x<3时,-(x-3)≤4
解这个不等式,得:x≥-1
由条件x<3,有:-1≤x<3
∴如图,综合(1)、(2)原不等式的解为:-1≤x≤7
根据以上思想,请探究完成下列2个小题:
(1)|x+1|≤2;
(2)|x-2|≥1.
分析 (1)分①x+1≥0,即x≥-1,②x+1<0,即x<-1,两种情况分别求解可得;
(2)分①x-2≥0,即x≥2,②x-2<0,即x<2,两种情况分别求解可得.
解答 解:(1)|x+1|≤2,
①当x+1≥0,即x≥-1时:x+1≤2,
解这个不等式,得:x≤1
由条件x≥-1,有:-1≤x≤1;
②当x+1<0,即 x<-1时:-(x+1)≤2
解这个不等式,得:x≥-3
由条件x<-1,有:-3≤x<-1
∴综合①、②,原不等式的解为:-3≤x≤1.
(2)|x-2|≥1
①当x-2≥0,即x≥2时:x-2≥1
解这个不等式,得:x≥3
由条件x≥2,有:x≥3;
②当x-2<0,即 x<2时:-(x-2)≥1,
解这个不等式,得:x≤1,
由条件x<2,有:x≤1,
∴综合①、②,原不等式的解为:x≥3或x≤1.
点评 本题主要考查绝对值不等式的求解,熟练掌握绝对值的性质分类讨论是解题的关键.

练习册系列答案
相关题目
11.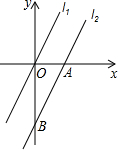 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x轴、y轴分别交于点A,B,且l1∥l2,OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x轴、y轴分别交于点A,B,且l1∥l2,OA=2,则线段OB的长为( )
 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x轴、y轴分别交于点A,B,且l1∥l2,OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x轴、y轴分别交于点A,B,且l1∥l2,OA=2,则线段OB的长为( )| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
8.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如下表:
(1)根据上表的数据,请你写出Q与t的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加满48L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
| 汽车行驶时间t/h | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q/L | 100 | 94 | 88 | 82 | … |
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加满48L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
 B.
B.  = ±3 C. (ab2)3= a3b6 D. a6÷a2 = a3
= ±3 C. (ab2)3= a3b6 D. a6÷a2 = a3 的值在( )
的值在( ) 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),则第4个正方形的边长为8,第n个正方形的边长为2n-1.
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),则第4个正方形的边长为8,第n个正方形的边长为2n-1.