题目内容
14．（1）已知关于x的一次函数y=（3a-7）x+a-2的图象与y轴交点在x轴的上方，且随x的增大而减小，求a的取值范围．（2）已知直线y=2x+1-2b和y=3x+b的交点在y轴上，求b的值．
分析 （1）依题意可得：3a-7＜0且a-2＞0，据此求出a的取值范围即可．
（2）依题意可得：1-2b=b，据此求出b的值是多少即可．
解答 解：（1）依题意可得：3a-7＜0且a-2＞0，
解得：2＜a＜$\frac{7}{3}$．
（2）依题意可得：1-2b=b，
解得：b=$\frac{1}{3}$．
点评 此题主要考查了两条直线相交的问题，以及一次函数的图象与系数的关系，要熟练掌握．
练习册系列答案
相关题目
B. 
C. 
D. 
2．“端午节”是中华民族古老的传统节日．甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案．
甲超市方案：购买该种粽子超过200元后，超出200元的部分按95%收费；
乙超市方案：购买该种粽子超过300元后，超出300元的部分按90%收费．
设某位顾客购买了x元的该种粽子．
（1）补充表格，填写在“横线”上：
（2）列式计算说明，如果顾客在“端午节”当天购买该种粽子超过200元，那么到哪家超市花费更少？
甲超市方案：购买该种粽子超过200元后，超出200元的部分按95%收费；
乙超市方案：购买该种粽子超过300元后，超出300元的部分按90%收费．
设某位顾客购买了x元的该种粽子．
（1）补充表格，填写在“横线”上：
| x （单位：元） | 实际在甲超市的花费 （单位：元） | 实际在乙超市的花费 （单位：元） |
| 0＜x≤200 | x | x |
| 200＜x≤300 | 10+0.95x | x |
| x＞300 | 10+0.95x | 30+0.9x |
9．科学家发现一种病毒的直径约为0.0000403m，用科学记数法表示为（ ）
| A． | 4.03×105 | B． | 4.03×10-5 | C． | 4.03×10-6 | D． | 4.03×10-7 |
阅读：
6．平面直角坐标系中，三条直线l1：y=ax，l2：y=x-a，l3：y=a（a≠0）的公共点是（ ）
| A． | （-1，-$\frac{1}{2}$） | B． | （-$\frac{1}{2}$，-1） | C． | （$\frac{1}{2}$，1） | D． | （1，$\frac{1}{2}$） |
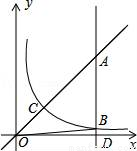
如图，在?ABCD中，CH⊥AD于点H，CH与BD的交点为E，如果∠1=70°，∠ABC=3∠2，那么∠ADC=60°．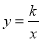
（x＞0）上一点，直线AB平行于y轴交直线y=x于点A，交x轴于点D， 
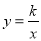与直线y=x交于点C，若OB2﹣AB2=4