��Ŀ����
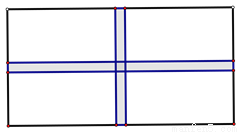
ijУ�ķ�У���滮ʱ�����ڳ�Ϊ32�ף���Ϊ20�ij����β�ƺ��������ͬ�������������ഹֱ��С·���ѳ����β�ƺ�ָ��ͬ������ĵ��Ŀ�С��ƺ��ÿ��С��ƺ�����Ϊ135ƽ���ף��ʵ�·�Ŀ��Ƕ����ף�
��ϰ��ϵ�д�
 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
�����Ŀ
��Ŀ����
ijУ�ķ�У���滮ʱ�����ڳ�Ϊ32�ף���Ϊ20�ij����β�ƺ��������ͬ�������������ഹֱ��С·���ѳ����β�ƺ�ָ��ͬ������ĵ��Ŀ�С��ƺ��ÿ��С��ƺ�����Ϊ135ƽ���ף��ʵ�·�Ŀ��Ƕ����ף�

 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�