题目内容
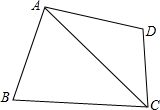 如图,四边形ABCD中AD=AB,∠DAB+∠BCD=180°,求证:CA平分∠DCB.
如图,四边形ABCD中AD=AB,∠DAB+∠BCD=180°,求证:CA平分∠DCB.考点:全等三角形的判定与性质
专题:证明题
分析:作AE⊥BC,AF⊥CD延长线于F点,易证∠B=∠ADF,即可证明△ABE≌△ADF,可得AE=AF,即可证明RT△ACE≌RT△ACF,可得∠ACB=∠ACD,即可解题.
解答:证明:作AE⊥BC,AF⊥CD延长线于F点,
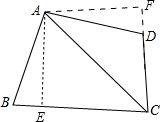
∵∠DAB+∠BCD=180°,
∴∠B+∠ADC=180°,
∵∠ADC+∠ADF=180°,
∴∠B=∠ADF,
∵在△ABE和△ADF中,
,
∴△ABE≌△ADF,(AAS)
∴AE=AF,
∵在RT△ACE和RT△ACF中,
,
∴RT△ACE≌RT△ACF,(HL)
∴∠ACB=∠ACD,
∴CA平分∠DCB.

∵∠DAB+∠BCD=180°,
∴∠B+∠ADC=180°,
∵∠ADC+∠ADF=180°,
∴∠B=∠ADF,
∵在△ABE和△ADF中,
|
∴△ABE≌△ADF,(AAS)
∴AE=AF,
∵在RT△ACE和RT△ACF中,
|
∴RT△ACE≌RT△ACF,(HL)
∴∠ACB=∠ACD,
∴CA平分∠DCB.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABE≌△ADF和RT△ACE≌RT△ACF是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 已知:如图,点P是△ABC的重心,过P作AC的平行线,分别交AB,BC于点D,E,作DF∥EC,交AC于点F,若△ABC的面积为18cm2,求四边形ECFD的面积.
已知:如图,点P是△ABC的重心,过P作AC的平行线,分别交AB,BC于点D,E,作DF∥EC,交AC于点F,若△ABC的面积为18cm2,求四边形ECFD的面积. 如图,∠1=∠E,∠2与∠C互余,DB⊥AC于点F.试确定图中互相平行的直线,并说明理由.
如图,∠1=∠E,∠2与∠C互余,DB⊥AC于点F.试确定图中互相平行的直线,并说明理由.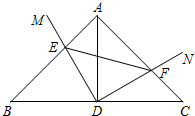 如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.
如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.