题目内容
解方程:
(1)3x-7+4x=5x-3
(2)
-
=1
(3)2(x-2)-8(x-1)=3(1-x)
(4)x-
=
-3.
(1)3x-7+4x=5x-3
(2)
| x |
| 2 |
| x-1 |
| 3 |
(3)2(x-2)-8(x-1)=3(1-x)
(4)x-
| x-2 |
| 5 |
| 2x-5 |
| 3 |
考点:解一元一次方程
专题:
分析:按照解一元一次方程的步骤与方法求得x的数值即可.
解答:(1)3x-7+4x=5x-3
解:3x-4x-5x=-3+7
-6x=4
x=-
;
(2)
-
=1
解:3x-2(x-1)=6
3x-2x+2=6
3x-2x=6-2
x=4;
(3)2(x-2)-8(x-1)=3(1-x)
解:2x-4-8x+8=3-3x
2x-8x+3x=3+4-8
-3x=-1
x=
;
(4)x-
=
-3
解:15x-3(x-2)=5(2x-5)-45
15x-3x+6=10x-25-45
15x-3x-10x=-25-45-6
2x=-76
x=-38.
解:3x-4x-5x=-3+7
-6x=4
x=-
| 2 |
| 3 |
(2)
| x |
| 2 |
| x-1 |
| 3 |
解:3x-2(x-1)=6
3x-2x+2=6
3x-2x=6-2
x=4;
(3)2(x-2)-8(x-1)=3(1-x)
解:2x-4-8x+8=3-3x
2x-8x+3x=3+4-8
-3x=-1
x=
| 1 |
| 3 |
(4)x-
| x-2 |
| 5 |
| 2x-5 |
| 3 |
解:15x-3(x-2)=5(2x-5)-45
15x-3x+6=10x-25-45
15x-3x-10x=-25-45-6
2x=-76
x=-38.
点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
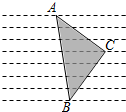 如图,在△ABC中,∠ACB=90°,AC=BC,顶点A、B、C恰好分别落在一组平行线中的三条直线上,若相邻两条平行线间的距离是2个单位长度,则△ABC的面积是( )
如图,在△ABC中,∠ACB=90°,AC=BC,顶点A、B、C恰好分别落在一组平行线中的三条直线上,若相邻两条平行线间的距离是2个单位长度,则△ABC的面积是( )| A、24 | B、48 | C、50 | D、100 |
若关于的x的分式方程
-1=
有增根,则k可能是( )
| x+1 |
| x-1 |
| k |
| x2-1 |
| A、-1 | B、1 | C、0 | D、2 |
如果一个多项式的次数是5,那么这个多项式的任何一项的次数满足( )
| A、都小于5 | B、都大于5 |
| C、都不小于5 | D、都不大于5 |
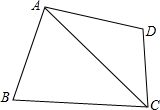 如图,四边形ABCD中AD=AB,∠DAB+∠BCD=180°,求证:CA平分∠DCB.
如图,四边形ABCD中AD=AB,∠DAB+∠BCD=180°,求证:CA平分∠DCB.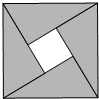 如图是我国古代数学家赵爽的“勾股方圆图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是12,小正方形的面积是2,直角三角形的两直角边分别是a和b,求(a+b)2的值.
如图是我国古代数学家赵爽的“勾股方圆图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是12,小正方形的面积是2,直角三角形的两直角边分别是a和b,求(a+b)2的值. 如图所示的图形是一个中心对称图形,点O是AC与BD的交点,且是对称中心.
如图所示的图形是一个中心对称图形,点O是AC与BD的交点,且是对称中心.