题目内容
20.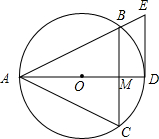 已知等边△ABC内接于⊙O,AD为O的直径交线段BC于点M,DE∥BC,交AB的延长线于点E.
已知等边△ABC内接于⊙O,AD为O的直径交线段BC于点M,DE∥BC,交AB的延长线于点E.(1)求证:DE是⊙O的切线;
(2)若等边△ABC的边长为6,求BE的长.
分析 (1)由等边三角形的性质得出O即是△ABC的外心,又是△ABC的内心,得出∠BAM=∠CAM=30°,因此∠AMB=90°,由平行线的性质得出∠EDA=90°,即可得出结论;
(2)由等边三角形的性质得出BM=$\frac{1}{2}$AB=3,连接OB,则∠OBM=30°,得出OM=$\frac{1}{2}$OB,由勾股定理求出OB,由平行线的性质得出$\frac{AB}{AE}$=$\frac{AM}{AD}$,求出AE,即可得出BE的长.
解答 (1)证明:∵等边△ABC内接于⊙O,
∴∠ABC=60°,O即是△ABC的外心,又是△ABC的内心,
∴∠BAM=∠CAM=30°,
∴∠AMB=90°,
∵DE∥BC,
∴∠EDA=∠AMB=90°,
∵AD为⊙O的直径,
∴DE是⊙O的切线;
(2)解: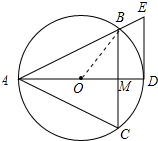 ∵△ABC是等边三角形,
∵△ABC是等边三角形,
∴BM=$\frac{1}{2}$AB=3,
连接OB,如图所示:
则∠OBM=30°,
∴OM=$\frac{1}{2}$OB,
由勾股定理得:OB2-OM2=BM2,
即OB2-($\frac{1}{2}$OB)2=32,
解得:OB=2$\sqrt{3}$,
∴OM=$\sqrt{3}$,AM=3$\sqrt{3}$,AD=4$\sqrt{3}$,
∵DE∥BC,
∴$\frac{AB}{AE}$=$\frac{AM}{AD}$,即$\frac{6}{AE}$=$\frac{3\sqrt{3}}{4\sqrt{3}}$,
解得:AE=8,
∴BE=AE-AB=8-6=2.
点评 本题考查了切线的判定、等边三角形的性质、平行线的性质、勾股定理等知识;熟练掌握切线的判定和等边三角形的性质,由勾股定理求出半径是解决问题的突破口.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,在△ABC中,点I是外心,∠BIC=110°,则∠A=55°.
如图,在△ABC中,点I是外心,∠BIC=110°,则∠A=55°.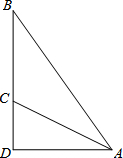 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m.
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m.