题目内容
某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每一辆车可装甲种特产8吨,或者乙种特产6吨,或者丙种特产5吨.每辆汽车只能装运同一种土特产,且必须装满,甲、乙、丙三种土特产每吨的利润分别为1200元、1600元、1000元,根据提供的信息,解答以下问题.
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式.
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案.
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值.
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式.
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案.
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值.
考点:一次函数的应用,一元一次不等式组的应用
专题:
分析:(1)根据计划的车辆数20表示出运乙种土特产的车辆数,然后根据运往外地的土特产共120吨列式整理即可;
(2)根据车辆都不少于3辆列不等式求出x的取值范围,再根据车辆数是正整数设计安排方案;
(3)设销售获利为W,然后列式整理得到W的表达式,再根据一次函数的增减性求出最大利润.
(2)根据车辆都不少于3辆列不等式求出x的取值范围,再根据车辆数是正整数设计安排方案;
(3)设销售获利为W,然后列式整理得到W的表达式,再根据一次函数的增减性求出最大利润.
解答:解:(1)由题意得,8x+6y+5(20-x-y)=120,
整理得,y=-3x+20;
(2)∵装运每种土特产的车辆都不少于3辆,
∴-3x+20≥3,
解得x≤
,
∴3≤x≤
,
∵x表示车辆数,为正整数,
∴x=3、4、5,
所以,有以下几种安排方案:
方案一:装运甲种土特产3辆,装运乙种土特产11辆,装运丙种土特产6辆,
方案二:装运甲种土特产4辆,装运乙种土特产8辆,装运丙种土特产8辆,
方案三:装运甲种土特产5辆,装运乙种土特产5辆,装运丙种土特产10辆;
(3)设销售获利为W,
则W=1200x+1600y+1000(20-x-y),
=200x+600y+20000,
=200x+600(-3x+20)+20000,
=-1600x+32000,
∵-1600<0,
∴W随x的增大而减小,
∴当x=3时,销售获利最大,
最大利润值为-1600×3+32000=27200元.
整理得,y=-3x+20;
(2)∵装运每种土特产的车辆都不少于3辆,
∴-3x+20≥3,
解得x≤
| 17 |
| 3 |
∴3≤x≤
| 17 |
| 3 |
∵x表示车辆数,为正整数,
∴x=3、4、5,
所以,有以下几种安排方案:
方案一:装运甲种土特产3辆,装运乙种土特产11辆,装运丙种土特产6辆,
方案二:装运甲种土特产4辆,装运乙种土特产8辆,装运丙种土特产8辆,
方案三:装运甲种土特产5辆,装运乙种土特产5辆,装运丙种土特产10辆;
(3)设销售获利为W,
则W=1200x+1600y+1000(20-x-y),
=200x+600y+20000,
=200x+600(-3x+20)+20000,
=-1600x+32000,
∵-1600<0,
∴W随x的增大而减小,
∴当x=3时,销售获利最大,
最大利润值为-1600×3+32000=27200元.
点评:本题考查了一次函数的应用,一元一次不等式的应用,主要是利用一次函数的增减性求出最值问题,要注意装运丙种土特产的车辆数的表示.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
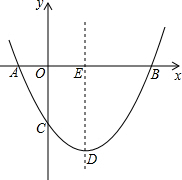 如图,抛物线y=
如图,抛物线y=| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 某中学五班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人.
某中学五班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人.