题目内容
3.先化简,再求值:$\frac{1}{4}$(4a2-2a-8)-($\frac{1}{2}$a-1),其中a=1.分析 先化简然后将a的值代入即可求出答案.
解答 解:当a=1时,
原式=a2-$\frac{1}{2}$a-2-$\frac{1}{2}$a+1
=a2-a-1
=1-1-1
=-1
点评 本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
8.某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
估计这批苹果损坏的概率为0.1(结果保留小数点后一位),损坏的苹果约有1000kg.
| 苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
| 损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
| 苹果损坏的频率$\frac{m}{n}$(结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
15.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (-3)2=6 | C. | (-a3)2=a6 | D. | a2+a3=a5 |
13.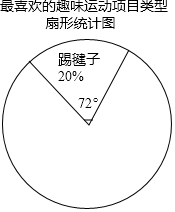 某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
(1)直接写出a=0.25,b=40;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
 某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
| 项目类型 | 频数 | 频率 |
| 跳长绳 | 25 | a |
| 踢毽子 | 20 | 0.2 |
| 背夹球 | b | 0.4 |
| 拔河 | 15 | 0.15 |
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
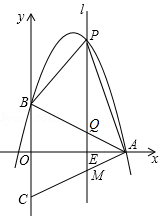 如图,在等腰△ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=ax2+$\frac{7}{2}$x+c经过A(8,0)、B(0,4)两点.
如图,在等腰△ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=ax2+$\frac{7}{2}$x+c经过A(8,0)、B(0,4)两点.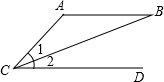 如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是1.
如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是1.