题目内容
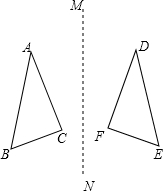 如图,△ABC与△DEF关于直线MN对称,其中∠C=90°,AC=8cm,DE=10cm,BC=6cm.
如图,△ABC与△DEF关于直线MN对称,其中∠C=90°,AC=8cm,DE=10cm,BC=6cm.(1)线段AD与MN的关系是什么?
(2)求∠F的度数;
(3)求△ABC的周长和△DEF的面积.
考点:轴对称的性质
专题:
分析:(1)利用关于某条直线对称的两个图形的对称点的连线被对称轴垂直平分可以得到;
(2)利用关于某条直线对称的三角形全等可以得到对应角相等;
(3)利用关于某条直线对称的三角形全等可以得到周长和面积相等;
(2)利用关于某条直线对称的三角形全等可以得到对应角相等;
(3)利用关于某条直线对称的三角形全等可以得到周长和面积相等;
解答:解:(1)∵△ABC与△DEF关于直线MN对称,
∴MN垂直平分AD;
(2)∵△ABC与△DEF关于直线MN对称,
∴△ABC≌△DEF,
∵∠C=∠F=90°;
(3)∵AC=8cm,DE=10cm,BC=6cm,
∴DE=AB=10cm,
∴△ABC的周长=6+8+10=24cm;
△DEF的面积=
×6×8=24cm2.
∴MN垂直平分AD;
(2)∵△ABC与△DEF关于直线MN对称,
∴△ABC≌△DEF,
∵∠C=∠F=90°;
(3)∵AC=8cm,DE=10cm,BC=6cm,
∴DE=AB=10cm,
∴△ABC的周长=6+8+10=24cm;
△DEF的面积=
| 1 |
| 2 |
点评:本题考查了轴对称图形的性质,解题的关键是了解关于某条直线对称的两个图形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将△ABC的三个顶点坐标的横坐标乘以-1,纵坐标不变,则所得图形与原图形的关系是( )
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、绕原点旋转了180° |
| D、向x轴负方向平移了1个单位 |
下列各式中,最简二次根式是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
以下列各组数为三角形的边长,能构成直角三角形的是( )
| A、8,1,17 |
| B、3,5,7 |
| C、6,8,10 |
| D、5,10,12 |
已知四边形ABCD是平行四边形,下列结论中不正确的是( )
| A、当AB=BC时,它是菱形 |
| B、当AC=BD时,它是正方形 |
| C、当AC⊥BD时,它是菱形 |
| D、当∠ABC=90°时,它是矩形 |
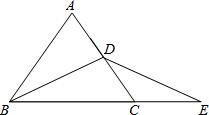 如图,在△ABC中,BA=BC,BD⊥AC,延长BC至点E,恰使CE=CD,BD=DE,求证:△ABC是等边三角形.
如图,在△ABC中,BA=BC,BD⊥AC,延长BC至点E,恰使CE=CD,BD=DE,求证:△ABC是等边三角形.