题目内容
13.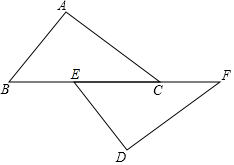 如图,已知点B、E、C、F在一条直线上,AC∥DE,AC=DE,∠A=∠D.
如图,已知点B、E、C、F在一条直线上,AC∥DE,AC=DE,∠A=∠D.(1)求证:AB=DE;
(2)若BC=9,EC=5,求BF的长.
分析 (1)由条件证明△ABC≌△DFE即可求得AB=DF;
(2)由全等三角形的性质可得BC=FE,再利用线段的长和差可求得BF.
解答 (1)证明:
∵AC∥DE,
∴∠ACB=∠DEF,
在△ABC和△DFE中
$\left\{\begin{array}{l}{∠ACB=∠DEF}\\{AC=DE}\\{∠A=D}\end{array}\right.$
∴△ABC≌△DFE(ASA),
∴AB=DF;
(2)解:
∵△ABC≌△DFE,
∴BC=FE,
∴BC-EC=FE-EC,
∴EB=CF=BE-EC=9-5,
∴BF=BC+CF=9+4=13
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和性质(即全等三角形的对应边相等、对应角相等)是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
1.下列运算正确的是( )
| A. | -a+b+c+d=-(a-b)-(-c-d) | B. | x-(y-z)=x-y-z | ||
| C. | x+2y-2z=x-2(z+y) | D. | -(x-y+z)=-x-y-z |
 唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云: 如图,C,D是线段AB上两点,D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长等于多少?
如图,C,D是线段AB上两点,D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长等于多少? 如图,在△ABC中,BD⊥AC,垂足为D,AB=AC=9,BC=6,求BD的长.
如图,在△ABC中,BD⊥AC,垂足为D,AB=AC=9,BC=6,求BD的长.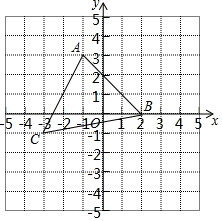 如图,在平面直角坐标系中有一个△ABC,顶点A(-1,3),B(2,0),C(-3,-1).
如图,在平面直角坐标系中有一个△ABC,顶点A(-1,3),B(2,0),C(-3,-1). 已知:如图,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连结BC′,求BC′的长.
已知:如图,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连结BC′,求BC′的长.