题目内容
12. 如图,平行四边形ABCD中,E,F分别是BA,DC延长线上的点,且AE=CF,过E作EM⊥BE交AD于点M,过F作FN⊥DF交BC于点N.求证:AM=CN.
如图,平行四边形ABCD中,E,F分别是BA,DC延长线上的点,且AE=CF,过E作EM⊥BE交AD于点M,过F作FN⊥DF交BC于点N.求证:AM=CN.
分析 直接利用平行四边形的性质得出∠EAM=∠FCN,∠E=∠F,进而利用全等三角形的判定与性质得出答案.
解答 证明:∵在平行四边形ABCD中,∠BAD=∠BCD,
∴∠EAM=∠FCN,
∵EM⊥BE,FN⊥DF,
∴∠E=∠F,
在△EAM和△FCN中
$\left\{\begin{array}{l}{∠EAM=∠FCN}\\{AE=CF}\\{∠E=∠F}\end{array}\right.$,
∴△EAM≌△FCN(ASA),
∴AM=CN.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质,得出△EAM≌△FCN是解题关键.

练习册系列答案
相关题目
3.某中学为筹备校庆活动,准备印制一批校庆纪念册,该纪念册每册需要10张8K大小的纸,其中4张为彩色页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩色页300元/张,黑白页50元/张;印刷费与印数的关系见表.
(1)直接写出印制这批纪念册的制版费为多少元;
(2)若印制6千册,那么共需多少费用?
(3)如印制x(1≤x<10)千册,所需费用为y元,请写出y与x之间的关系式.
| 印数a (单位:千册) | 1≤a<5 | 5≤a<10 |
| 彩色 (单位:元/张) | 2.2 | 2.0 |
| 黑白(单位:元/张) | 0.7 | 0.6 |
(2)若印制6千册,那么共需多少费用?
(3)如印制x(1≤x<10)千册,所需费用为y元,请写出y与x之间的关系式.
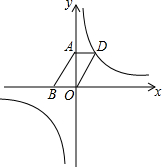 如果已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在平面直角坐标系的第一、三象限,若该反比例函数的图象经过平行四边形ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0).
如果已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在平面直角坐标系的第一、三象限,若该反比例函数的图象经过平行四边形ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0). 已知:如图,AB∥CD,EF分别交AB、CD于点E,F,EH,FG分别平分∠AEF,∠DFE,则EH∥FG,请用推理的方法说明它是真命题.
已知:如图,AB∥CD,EF分别交AB、CD于点E,F,EH,FG分别平分∠AEF,∠DFE,则EH∥FG,请用推理的方法说明它是真命题.