题目内容
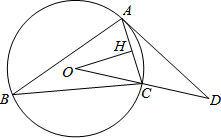 已知:如图,△ABC内接于⊙O,OH⊥AC于H,∠B=30°,过A点的直线与OC的延长线交于点D,∠CAD=30°,AD=10
已知:如图,△ABC内接于⊙O,OH⊥AC于H,∠B=30°,过A点的直线与OC的延长线交于点D,∠CAD=30°,AD=10| 3 |
(1)求证:AD是⊙O的切线;
(2)若E为⊙O上一动点,连接AE交直线OD于点P,问:是否存在点P,使得PA+PH的值最小?若存在求PA+PH的最小值;若不存在,说明理由.
考点:切线的判定
专题:证明题
分析:(1)连结OA,如图,根据圆周角定理得∠AOC=2∠B=60°,则可判断△OAC为等边三角形,所以∠OAC=60°,则∠OAD=∠CAD+∠OAC=90°,于是可根据切线的判定定理得到AD是⊙O的切线;
(2)在Rt△OAD中利用含30度的直角三角形三边的关系得到OA=
AD=10,则AC=OA=10;作弦AF⊥OC,连结HF交OD于P,延长AP交⊙O于E点,根据垂径定理得到OC平分AF,即OC垂直平分AF,则PA=PF,所以PA+PH=PF+PH=HF,根据两点之间线段最短得此时PA+PH的值最小;再利用垂径定理由OH⊥AC得HC=AH=5,FC=AC=10,∠OCF=∠OCA=60°,所以∠HCF=120°,在Rt△HCG中计算出CG=
HC=
,HG=
CG=
,然后在Rt△HFG中,根据勾股定理可计算出HF.
(2)在Rt△OAD中利用含30度的直角三角形三边的关系得到OA=
| ||
| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
5
| ||
| 2 |
解答:(1)证明:连结OA,如图,
∵∠AOC=2∠B=2×30°=60°,
∴△OAC为等边三角形,
∴∠OAC=60°,
而∠CAD=30°,
∴∠OAD=∠CAD+∠OAC=90°,
∴OA⊥AD,
∴AD是⊙O的切线;
(2)解:存在.
在Rt△OAD中,∵∠AOD=60°,∠D=30°,
∴OA=
AD=
×10
=10,
∴AC=OA=10,
作弦AF⊥OC,连结HF交OD于P,延长AP交⊙O于E点,
∵OC⊥AF,
∴OC平分AF,即OC垂直平分AF,
∴PA=PF,
∴PA+PH=PF+PH=HF,
∴此时PA+PH的值最小,
∵OH⊥AC,
∴HC=AH=5,
∵OC⊥AF,
∴AC弧=FC弧,
∴FC=AC=10,∠OCF=∠OCA=60°,
∴∠HCF=120°,
作HG⊥FC于G,如图,
在Rt△HCG中,∠HCG=60°,HC=5,
∴CG=
HC=
,
HG=
CG=
,
在Rt△HFG中,FG=FC+CG=
,HG=
,
∴HF=
=
=5
,
即PA+PH的最小值为5
.
∵∠AOC=2∠B=2×30°=60°,
∴△OAC为等边三角形,
∴∠OAC=60°,
而∠CAD=30°,
∴∠OAD=∠CAD+∠OAC=90°,
∴OA⊥AD,

∴AD是⊙O的切线;
(2)解:存在.
在Rt△OAD中,∵∠AOD=60°,∠D=30°,
∴OA=
| ||
| 3 |
| ||
| 3 |
| 3 |
∴AC=OA=10,
作弦AF⊥OC,连结HF交OD于P,延长AP交⊙O于E点,
∵OC⊥AF,
∴OC平分AF,即OC垂直平分AF,
∴PA=PF,
∴PA+PH=PF+PH=HF,
∴此时PA+PH的值最小,
∵OH⊥AC,
∴HC=AH=5,
∵OC⊥AF,
∴AC弧=FC弧,
∴FC=AC=10,∠OCF=∠OCA=60°,
∴∠HCF=120°,
作HG⊥FC于G,如图,
在Rt△HCG中,∠HCG=60°,HC=5,
∴CG=
| 1 |
| 2 |
| 5 |
| 2 |
HG=
| 3 |
5
| ||
| 2 |
在Rt△HFG中,FG=FC+CG=
| 25 |
| 2 |
5
| ||
| 2 |
∴HF=
| HG2+FG2 |
(
|
| 7 |
即PA+PH的最小值为5
| 7 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了等边三角形的性质、勾股定理和含30度的直角三角形三边的关系.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
下列说法错误的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、2的平方根是±
|
若
与|x-y-3|互为相反数,则x+y的值为( )
| x-2y |
| A、3 | B、9 | C、12 | D、27 |