题目内容
10. 数学兴趣小组向利用所学的知识了解某广告牌的高度,已知CD=2m,经测量,得到其它数据如图所示,其中∠CAH=30°,∠DBH=60°,AB=10m,请你根据以上数据计算GH的长(要求计算结果保留根号,不取近似值)
数学兴趣小组向利用所学的知识了解某广告牌的高度,已知CD=2m,经测量,得到其它数据如图所示,其中∠CAH=30°,∠DBH=60°,AB=10m,请你根据以上数据计算GH的长(要求计算结果保留根号,不取近似值)
分析 首先构造直角三角形,得出AE=$\frac{\sqrt{3}}{3}$x+10,BE=$\frac{\sqrt{3}}{3}$x,进而求出x的长,进而得出GH的长.
解答 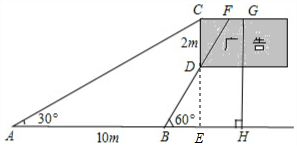 解:延长CD交AH于点E,
解:延长CD交AH于点E,
设DE=x,则BE=$\frac{\sqrt{3}}{3}$x,
∵∠A=30°,
∴$\frac{CE}{AE}=\frac{2+x}{10+\frac{\sqrt{3}}{3}x}$=$\frac{\sqrt{3}}{3}$,
∴x=5$\sqrt{3}$-3,
∴GH=EC=5$\sqrt{3}$-1(m)
答:GH的长为=(5$\sqrt{3}$-1)m.
点评 此题主要考查了解直角三角形的应用,根据已知构造直角三角形得出DE的长是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
5. 如图,在⊙O中,弦AC=2$\sqrt{3}$,点B是圆上一点,且∠ABC=45°,则⊙O的半径是( )
如图,在⊙O中,弦AC=2$\sqrt{3}$,点B是圆上一点,且∠ABC=45°,则⊙O的半径是( )
 如图,在⊙O中,弦AC=2$\sqrt{3}$,点B是圆上一点,且∠ABC=45°,则⊙O的半径是( )
如图,在⊙O中,弦AC=2$\sqrt{3}$,点B是圆上一点,且∠ABC=45°,则⊙O的半径是( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
20.已知a,b,c,d是成比例线段,其中a=2cm,b=3cm,c=4cm,则线段d的长是( )
| A. | 6cm | B. | 5cm | C. | $\frac{8}{3}$cm | D. | $\frac{3}{8}$cm |
 命题“同位角相等”是真命题吗?如果是,说出理由;如果不是,请举出反例.
命题“同位角相等”是真命题吗?如果是,说出理由;如果不是,请举出反例. 如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为$\frac{OB′}{OB}$=$\frac{2}{3}$,若五边形ABCDE的面积为15cm2,那么五边形A′B′C′D′E′的面积为$\frac{20}{3}$cm2.
如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为$\frac{OB′}{OB}$=$\frac{2}{3}$,若五边形ABCDE的面积为15cm2,那么五边形A′B′C′D′E′的面积为$\frac{20}{3}$cm2. 如图,△ABC三个顶点的坐标分别为A(-1,1),B(-4,2),C(-3,4).
如图,△ABC三个顶点的坐标分别为A(-1,1),B(-4,2),C(-3,4).