题目内容
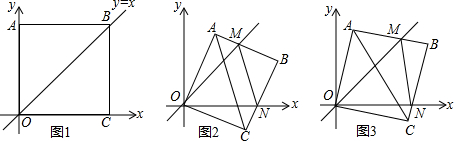
如图,在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,顶点O在原点(如图1).现将正方形OABC绕O点顺时针旋转一定角度,当A点第一次落在直线y=x上时停止旋转.旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.
(1)当点A第一次落在直线y=x上时停止旋转,此时图形旋转了 度;
(2)旋转过程中,当MN和AC平行时(如图2),求旋转角∠NOC的度数;
(3)设△MBN的周长为P,在旋转正方形OABC的过程中(如图3),P值是否变化?请判断并证明你的结论.
(1)当点A第一次落在直线y=x上时停止旋转,此时图形旋转了
(2)旋转过程中,当MN和AC平行时(如图2),求旋转角∠NOC的度数;
(3)设△MBN的周长为P,在旋转正方形OABC的过程中(如图3),P值是否变化?请判断并证明你的结论.

考点:一次函数综合题
专题:
分析:(1)A点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45°,OA旋转了45°;
(2)解决本题需利用全等,根据正方形一个内角的度数求出∠AOM的度数;
(3)利用全等把△MBN的各边整理到成与正方形的边长有关的式子.
(2)解决本题需利用全等,根据正方形一个内角的度数求出∠AOM的度数;
(3)利用全等把△MBN的各边整理到成与正方形的边长有关的式子.
解答:解:(1)∵A点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45°,
∴OA旋转了45°.
故答案为:45;
(2)∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°.
∴∠BMN=∠BNM.
∴BM=BN.
又∵BA=BC,
∴AM=CN.
又∵OA=OC,∠OAM=∠OCN,
在△OAM和△OCN中,
.
∴△OAM≌△OCN(SAS).
∴∠AOM=∠CON=
(∠AOC-∠MON)=(90°-45°)=2
2.5°.
∴旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为∠NOC=45°-22.5°=22.5°.
(3)在旋转正方形OABC的过程中,P值无变化.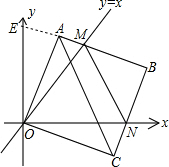
证明:延长BA交y轴于E点,
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN.
在△OAE和△OCN中,
.
∴△OAE≌△OCN(ASA).
∴OE=ON,AE=CN.
在△OME和△OMN中
.
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
∴P=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.
∴在旋转正方形OABC的过程中,P值无变化.
∴OA旋转了45°.
故答案为:45;
(2)∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°.
∴∠BMN=∠BNM.
∴BM=BN.
又∵BA=BC,
∴AM=CN.
又∵OA=OC,∠OAM=∠OCN,
在△OAM和△OCN中,
|
∴△OAM≌△OCN(SAS).
∴∠AOM=∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
∴旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为∠NOC=45°-22.5°=22.5°.
(3)在旋转正方形OABC的过程中,P值无变化.

证明:延长BA交y轴于E点,
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN.
在△OAE和△OCN中,
|
∴△OAE≌△OCN(ASA).
∴OE=ON,AE=CN.
在△OME和△OMN中
|
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
∴P=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.
∴在旋转正方形OABC的过程中,P值无变化.
点评:此题主要考查了旋转的性质以及全等三角形的判定与性质等知识,注意求一些线段的长度或角的度数,总要整理到已知线段的长度上或已知角的度数上进而得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列判断中正确的是( )
| A、四边相等的四边形是正方形 |
| B、四角相等的四边形是矩形 |
| C、对角线互相垂直的平行四边形是正方形 |
| D、对角线互相垂直的四边形是菱形 |
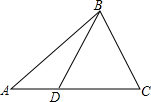 已知如图,在△ABC中,D是AC上一点,DC:BC=BC:AC=3:4,△BCD的周长是24cm,求:
已知如图,在△ABC中,D是AC上一点,DC:BC=BC:AC=3:4,△BCD的周长是24cm,求: 如图,AB为⊙O的直径,C为半圆的中点,⊙C的半径为2,AB=8,点P是直径AB上的一动点,PM与⊙C切于点M,则PM的取值范围为
如图,AB为⊙O的直径,C为半圆的中点,⊙C的半径为2,AB=8,点P是直径AB上的一动点,PM与⊙C切于点M,则PM的取值范围为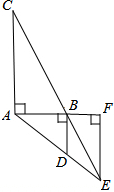 如图所示,CA⊥AB,DB⊥AB,AD与BC的延长线相交于点E,作EF⊥AB,交AB延长线于点F,且AC=p,BD=q,EF=r,AF=m,FB=n.求证:
如图所示,CA⊥AB,DB⊥AB,AD与BC的延长线相交于点E,作EF⊥AB,交AB延长线于点F,且AC=p,BD=q,EF=r,AF=m,FB=n.求证: 如图是由若干个大小相同的小正方体组成的几何体,从上面、左面、正面看会得到三个图形,其中看到的图形面积最小的是
如图是由若干个大小相同的小正方体组成的几何体,从上面、左面、正面看会得到三个图形,其中看到的图形面积最小的是