题目内容
在Rt△ABC中,∠C=90°,若sinA=
,则cosB的值是( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:同角三角函数的关系,互余两角三角函数的关系
专题:
分析:根据互余两角的三角函数关系进行解答.
解答:解:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=
,
∴cosB=
.
故选:B.
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=
| 3 |
| 5 |
∴cosB=
| 3 |
| 5 |
故选:B.
点评:本题考查了互余两角的三角函数关系,熟记关系式是解题的关键.在直角三角形中,∠A+∠B=90°时,正余弦之间的关系为:
①一个角的正弦值等于这个角的余角的余弦值,即sinA=(90°-∠A);
②一个角的余弦值等于这个角的余角的正弦值,即cosA=sin(90°-∠A);
也可以理解成若∠A+∠B=90°,那么sinA=cosB或sinB=cosA.
①一个角的正弦值等于这个角的余角的余弦值,即sinA=(90°-∠A);
②一个角的余弦值等于这个角的余角的正弦值,即cosA=sin(90°-∠A);
也可以理解成若∠A+∠B=90°,那么sinA=cosB或sinB=cosA.

练习册系列答案
相关题目
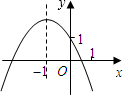 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a-b+c>1;③abc>0;④4a-2b+c<0;⑤c-a>1,其中所有正确结论的序号是( )
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a-b+c>1;③abc>0;④4a-2b+c<0;⑤c-a>1,其中所有正确结论的序号是( )| A、①②③⑤ | B、①③④ |
| C、①②③④ | D、①②③④⑤ |
 如图,用三角尺画出△ABC关于直线MN的轴对称图形.(不写作法,保留作图痕迹)
如图,用三角尺画出△ABC关于直线MN的轴对称图形.(不写作法,保留作图痕迹)



 如图,等边三角形ABC,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.若CE=BF,则∠EPF=
如图,等边三角形ABC,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.若CE=BF,则∠EPF=