Question

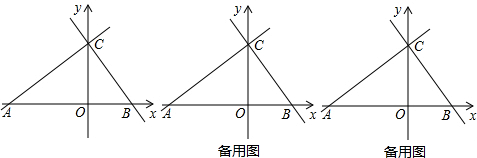
如图，AB∥CD，P为定点，E、F分别是AB、CD上的动点．

（1）求证：∠P=∠BEP+∠PFD；
（2）若M为CD上一点，如图2，∠FMN=∠BEP，且MN交PF于N．试说明∠EPF与∠PNM关系，并证明你的结论；
（3）移动E、F使得∠EPF=90°，如图3，作∠PEG=∠BEP，求∠AEG与∠PFD度数的比值．

Answer 1

考点：平行线的性质

专题：几何图形问题,证明题

分析：（1）如图1，过点P作PG∥AB，根据平行线的性质进行证明；
（2）利用（1）中的结果和三角形外角定理可以推知∠EPF=∠PNM；
（3）利用（1）中的结论得到∠1+∠2=90°，结合已知条件∠PEG=∠BEP，即∠1=∠3得到∠4=180°-2∠1，易求∠AEG与∠PFD度数的比值．

解答：（1）证明：如图1，过点P作PG∥AB．则∠1=∠BEP．
又∵AB∥CD，
∴PG∥CD，
∴∠2=∠PFD，
∴∠EPF=∠1+∠2=∠BEP+∠PFD，即∠EPF=∠BEP+∠PFD；

（2）∠EPF=∠PNM．理由如下：
由（1）知，∠EPF=∠BEP+∠PFD．
如图2，∵∠FMN=∠BEP，
∴∠EPF=∠FMN+∠PFD．
又∵∠PNM=∠FMN+∠PFD．
∴∠EPF=∠PNM；

（3）如图，∵由（1）知∠1+∠2=90°．
∴∠1=90°-∠2．
又∵∠1=∠3，
∴∠4=180°-2∠1=2∠2，
∴∠4：∠2=2：1．即∠AEG与∠PFD度数的比值为2：1．

点评：本题考查了平行线的性质．解答（2）、（3）题时，可以直接利用（1）的结论．