题目内容
5. 如图,△ACB≌△DCE,∠BCE=25°,则∠ACD的度数为( )
如图,△ACB≌△DCE,∠BCE=25°,则∠ACD的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
分析 根据△ACB≌△DCE可得出∠DCE=∠ACB,然后得到∠DCA=∠BCE,即可求得答案.
解答 解:∵△ACB≌△DCE,∠BCE=25°,
∴∠DCE=∠ACB,
∵∠DCE=∠DCA+∠ACE,∠ACB=∠BCE+∠ECA,
∴∠DCA+∠ACE=∠BCE+∠ECA,
∴∠DCA=∠BCE=25°,
故选:B.
点评 本题考查了全等三角形的性质的应用,能求出∠ACD=∠BCE是解此题的关键,注意:全等三角形的对应角相等.

练习册系列答案
相关题目
13.某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.表是某周的生产情况(超产记为正、减产记为负):
(1)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(2)请求出该工艺厂在本周实际生产工艺品的数量;
(3)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,若生产不足则每少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减(单位:个) | +1 | -2 | -7 | +12 | -15 | +10 | -9 |
(2)请求出该工艺厂在本周实际生产工艺品的数量;
(3)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,若生产不足则每少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
10.若方程(m-2)x2-3x-2=0是关于x的一元二次方程,则m的取值范围是( )
| A. | m>2 | B. | m≠2 | C. | m>0 | D. | m≠0 |
15.下列各组数中,互为相反数的一组是( )
| A. | -|-2|与$\root{3}{-8}$ | B. | -4与-$\sqrt{(-4)^{2}}$ | C. | -$\root{3}{2}$与$\root{3}{2}$ | D. | -$\sqrt{2}$与-$\sqrt{(-2)^{2}}$ |
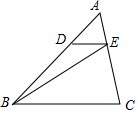 如图,△ABC中,D、E分别是边AB、AC 上的点,且∠DEB=∠EBC.
如图,△ABC中,D、E分别是边AB、AC 上的点,且∠DEB=∠EBC.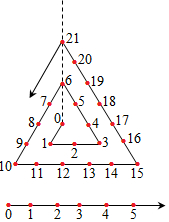 把一根起点为0的数轴弯折成如图所示的样子,虚线最下面第1个数字是0,往上第2个数字是6,第3个数字是21,…,则第5个数字是( )
把一根起点为0的数轴弯折成如图所示的样子,虚线最下面第1个数字是0,往上第2个数字是6,第3个数字是21,…,则第5个数字是( )